SVD算法是在Netflix竞赛中火起来的算法,当时这个算法夺冠了,然后带动起来一股研究浪潮,发展出了svd++,以及timeSvd等。
奇异值分解方法
SVD全称是奇异值分解,它是一种矩阵分解方法,大学线性代数里面也讲过奇异值分解的方法,但是老师当时没有说这东西有什么用,导致当时学的时候觉得很无聊,为什么要分解这东西。
首先我们知道推荐问题纯从行为来解就是一个矩阵填充问题,矩阵的一边是user,一边是item,如果某个u1对item_2有一个评分3,或者某个u2对某个物料item_4有一个点击,我们就可以给矩阵中填充一个3或者1,那么最终就形成一个大的稀疏矩阵,里面有行为的就会填充值,然后大多数没有填充值,我们需要做的就是给矩阵填上这些值,然后确定某个用户会对那些没看过的东西最感兴趣,然后做推荐。
矩阵分解方法
我们这里先说一下大学讲的奇异值分解的方法。
首先给一个mn的矩阵A,按照下面公式做分解,其中\(\Sigma\)是一个mn的矩阵,除对角线以为其他元素都是0,而对角线上的值就是所谓的奇异值。另外U是mm的酉矩阵,同样V是nn的酉矩阵,即满足\(U^T*U=I\)。
\[A = U \Sigma V^T\]- 将A的转置和A做矩阵乘法,这样就会得到一个n*n的方阵\(A^T*A\),然后运用方阵特征分解,得到\((A^T*A)*v_i = \lambda_i*v_i\)
- 得到矩阵\(A^T*A\)的n个特征值和对应的n个特征向量v,将所有特征向量v张成一个n*n的矩阵V,就是前面公式里的V矩阵,一般叫其中V中的每个特征向量是A的右奇异向量。
- 同样的对A和A的转置做乘法,就得到m*m的方阵\(A*A^T\),运用方阵特征分解,得到\((A*A^T)*u_i = \lambda_i*u_i\)
- 得到矩阵\(A*A^T\)的m个特征值和对应的m个特征向量u,将所有特征向量u张成一个m*m的矩阵U,就是前面公式里的U矩阵,一般叫U中的每个特征向量是A的左奇异向量。
- 计算奇异矩阵\(\Sigma\),\(A = U*\Sigma*V^T => A*U = U*\Sigma*V^T*V=> A*V = U*\Sigma => A*v_i = \sigma_i*u_i => \sigma_i = A*v_i/u_i\),这样得到奇异值\(\sigma\)组成奇异值矩阵\(\Sigma\)。
这是标准的按照线性代数理论进行分解的方法,时间复杂度是\(max(m,n)^3\),因为我们知道矩阵乘法时间复杂度就\(n^3\)。实际中工业上用这个时间复杂度太高了,因为物料数和用户数通常最少也是千万级别,三次方下来就10,0000亿,一个很恐怖的时间复杂度,先介绍一个SVD的性质,然后继续说怎么优化这个算法。
奇异值分解性质
对于中间奇异矩阵,它对角线上的值成为奇异值,是按照从大到小排序的,而且奇异值减少特别快,正常情况下前10%的奇异值占有了全部奇异值的99%,也就是说我们可以用前k个奇异值近似概括原始矩阵。
\[A_{m*N} = U_{m*m}*\Sigma_{m*n}*V_{n*n}^T \approx U_{m*k}*\Sigma_{k*k}*V_{k*n}^T\]这里\(k << min(m,n)\),起到的左右是数据压缩或者降维的作用。
分解算法优化
上面说到直接计算算法复杂度太高,没办法直接计算,但是从上面发现一个很好的性质,用前k的奇异值代替所有的,能够概括矩阵99%的特征,而\(k << min(m,n)\),那么我们可不可以利用这个性质呢。
首先我们不直接分解矩阵,而是用机器学习的方法,直接去求第二个矩阵,然后定义损失函数
\[C = \sum_{(i,j)\in{R}}[(a_{ij} - u_i*v_j^T)^2 + \lambda(u_i^2 + v_j^2)]\]前面一项使用平方差定义分解后和原始矩阵的RMSE,其中\(a_ij\)是原始矩阵的第i行第j列,而\(u_i\)是用户特征向量,\(v_j\)是物品特征向量,后面一项是正则化项。
有了损失函数我们就可以用ALS或者梯度下降法求解了,我们计算下上面的时间复杂度是O(mnk),而k是个很小的数,按照大O法则,复杂度就是O(m*n),这样在千万的数据上计算复杂度瞬间变成100亿了。
SVD算法
前面讲了奇异值分解的方法,当然最简单的方法就是直接把评分矩阵分解去做推荐,但是实际中发现不管是用户还是物品都存在一定偏差,比如有些用户给的评分就是比其他人高0.5,或者有些电影用户倾向于给高分,但是建模的时候没有考虑进去这种情况,改进后的算法任务评分 = 兴趣 + 偏见
\[a_{u,i} = u + b_u + b_i + U_u*V_i^T\]其中\(b_u\)表示用户偏见,\(b_i\)表示物品偏见,u表示全局均值,损失函数为:
\[C = \sum_{(u,i)\in{R}}(a_{u,i} - b_i - b_u - u_u*v_i^T)^2 + \lambda(\parallel {u_u} \parallel ^2 + \parallel{v_i}\parallel ^2 + b_u^2 + b_i^2)\]SVD++算法
实际使用中,除了用户或者物品偏见,还有一个问题就是行为数据中的评分数据很少,但是隐式行为数据有很多,那么我们能不能把隐式行为数据建模进去从而缓解评分稀疏提高推荐效果呢?
SVD++ 就是在SVD中加入了用户对物品的隐式行为,SVD++的假设条件是评分 = 显式兴趣 + 隐式兴趣 + 偏见
\[a_{u,i} = u + b_i + b_u + v_i^T * (u_u + \mid{I_u}\mid^{-\frac{1}{2}}* \sum_{j\in I_u}{y_j})\]其中\(I_u\)是该用户有隐式行为的所有物品集合,而\(y_j\)是隐式评分电影j反应出的喜好值,其中对\(I_u\)取根号是一个经验值,这样就把系统中大量的隐式行为也建模到SVD算法中,虽然这么做对计算复杂度提高了不少,同样的,损失函数为:
\[\begin{equation} \begin{split} C = \sum_{(u,i)\in{R}}(a_{u,i} - u - b_u - b_i - v_i^T* (u_u + \min I_u \mid^{-\frac{1}{2}}\sum_{j \in I_u}y_j))^2 \\ + \lambda(\sum_u(bi_u^2 + \parallel{u_u}\parallel^2) + \sum_i(b_i^2 + \parallel{v_i}\parallel^2 + \parallel{y_j}\parallel^2))) \end{split} \end{equation}\]timeSVD算法
到了2010年,koren发现在Netflix的数据中,个体用户的兴趣会随着时间转移,论文中称作concepte drift(观念转移)。比如大家都知道的《大话西游》,刚上映票房很低,大家都给出的评分也不高,但是随着时间流逝,大家给出的评分越来越高。另外可能有些电影在某些特定的节日或者某天会获得高分,作者希望建立模型能捕捉到这些。
timeSVD 就是在SVD中加入了时间因素,也可以叫做有时序的SVD,timeSVD的假设条件是评分 = 显式兴趣 + 时序兴趣 + 热点 + 偏见
我们按照原始论文的介绍来说,详见参考3,这个模型的为了对观念转移建模。从三个角度出发,首先式时间窗口概念,另外是实例权重,采用时间衰减,最后是集成学习的概念,引入多个基础预估方法。
static predictor 首先最基础的预估方法
\[b_{ui}(t) = u + b_u + b_i \tag{1}\]mov predictor 然后是mov方案
\[b_{ui}(t) = u + b_u + b_i + b_{i,Bin(t)} \tag{2}\]这里对\(b_i\)做了处理似的原来\(b_i(t) = b_i + b_{i,Bin(t)}\),分为Static和time changing两部分,引入物品的时间变化因素,对时间片进行划分,论文中是以10周为一片,共划分了30片,赋予一个\(Bin(t)\),即1-30之间。时间片划分也可以是其他的,小的时间片可以有更好的性能,大的时间片能够让每片有更多的数据。
linear predictor,引入对用户兴趣的变化,首先定义
\[dev_u(t) = sign(t-t_u) * \vert{t-t_u}\vert^\beta\]表示当前用户当前评分时间和平均评分时间的距离,这里用平均评分时间而不是当前时间,感觉有点小疑问,另外论文中\(\beta = 0.4\)
然后对\(b_u\)引入时间变化到线性模型,其中多了一个需要训练的参数\(\alpha\)
\[b_u^{(1)} = b_u + \alpha_u * dev_{u}(t)\]引入到公式中得到
\[b_{ui}(t) = u + b_u + \alpha_u * dev_u(t) + b_i + b_{i,Bin(t)} \tag{3}\]spline predictor 通过另一种方法引入用户兴趣变化到模型,这区别前面的线性模型是一个曲线式模型
\[b_{ui}(t) = u + b_u + \frac{\sum_{l=1}^{k_u} e^{-r\vert{t-t_l^u}\vert} * b_{t_l}^u}{\sum_{l=1}^{k_u} e^{-r\vert{t-t_l^u}\vert}} + b_i + b_{i,Bin(t)} \tag{4}\]linear+ predictor 引入实时特定,比如用户某天心情,或者生日等,引入一个参数\(b_{u,t}\),表示每日的特定偏差
\[b_{ui}(t) = u + b_u + \alpha_u * dev_u(t) + b_{u,t} + b_i + b_{i,Bin(t)} \tag{5}\]spline+ predictor 同样曲线模型也引入
\[b_{ui}(t) = u + b_u + \frac{\sum_{l=1}^{k_u} e^{-r\vert{t-t_l^u}\vert} * b_{t_l}^u}{\sum_{l=1}^{k_u} e^{-r\vert{t-t_l^u}\vert}} + b_{u,t} + b_i + b_{i,Bin(t)} \tag{6}\]通过梯度下降法进行训练,损失函数为
\[C = \sum_{u,i,t \in \mathcal{K}} (r_{ui}(t) - u - b_u - \alpha_u*dev_u(t) - b_{u,t} - b_i - b_{i,Bin(t)})^2 + \lambda(b_u^2 + \alpha_u^2 + b_{u,t}^2 + b_i^2 + b_{i,Bin(t)}^2)\]下表是原论文中对各个predictor用RMSE作为指标的结果
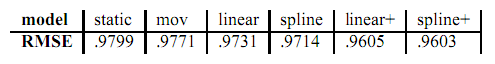
这里通过时序建模,对于用户矩阵的参数表示为下面式子:
\[u_u(t)[k] = p_{uk} + \alpha_{uk}*dev_u(t) + p_{utk} k = 1,....,f \tag{7}\]这里k代表第k个predictor,每一个predictor单独训练,最终得到如下公式,其中\(b_i(t),b_u(t)\)参见前面公式2,3表示
\[a_{u,i} = u + b_i(t) + b_u(t) + v_i^T * (u_u(t) + \mid{I_u}\mid^{-\frac{1}{2}}* \sum_{j\in I_u}{y_j})\]通过在Netflix数据集测试,对比三种算法,可以得到
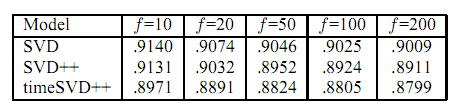
参考文献
- 奇异值分解(SVD)原理与在降维中的应用
- 基于ALS矩阵分解的协同过滤算法与源码分析
- 2010-Collaborative filtering with temporal dynamics
- Collaborative Filtering with Temporal Dynamics论文分析