算法类
逻辑回归原理及公式推导
逻辑回归通常是实习及1-3年初级算法必问的,最好能够很通顺的讲下来,里面公式都能够完整的推导下来,详细参见 读完之后重点关注回答两个问题:
- 有很多函数可以做到把一个数映射到0-1之间,为什么逻辑回归或者很多模型都选择在最后一层过sigmod函数
- 二分类损失函数log loss怎么来的
逻辑回归和线性回归的区别和联系
| Item | 线性回归 | 逻辑回归 |
|---|---|---|
| 解决问题 | 回归预测 | 分类 |
| 分布 | 正态分布 | 二项分布 |
| 损失函数 | 均方差 | logstic |
| 变量要求 | 连续性变量 | 分类型变量 |
| 线性/非线性 | 线性 | 不一定 |
联系:它们都属于广义线性模型,逻辑回归通过定义几率(odds),\(ln \frac{y}{1-y} = w^Tx\),然后通过log函数变换跟线性回归联系起来,\(w^Tx\)越大,则y>0.5,越小则y<0.5,然后就可以做分类。
L0和L1以及L2正则化区别
L0范数基本上不常见,表示向量中非零元素的个数,\(L_0\) = 0/1 with \(x_i \neq 0\),因为L1范数在一定程度上表示了L0范数的作用,所以这个不常用
L1范数表示向量中元素绝对值的和,\(L_1\) = \(\sum_{i=1}^{n} \mid x_i \mid\),L1范数解通常是稀疏性的,通常会让解比较极端,而且有特征选择的作用。
L2范数表示欧氏距离,\(L2 = \sqrt{\sum_{i=1}{n} x_i^2}\),L2范数有特征平滑作用,能够防止过拟合,能够限制每个特征解都比较小,但是不会让他变成0,并且能够让优化过程稳定且快速。
至于为什么L1范数的解会导致稀疏性,可以从两个维度分析,第一个维度是L1正则化相当于给损失函数中引入了拉普拉斯先验,看拉普拉斯分布图会发现它在0处是非平滑的;而L2正则化相当于给损失函数引入了高斯先验,看高斯分布图会发现它是个平滑函数,0处似乎极值,所以只会趋近0不会导致为0。第二个角度是带正则化和带约束的优化是等价的,使用拉格朗日函数,可以看到后面部分就是它的解空间,L2对应的是圆形解空间,L1对应的是菱形接空间,和目标函数更容易碰撞到边界上。
集成学习bagging和boosting的区别和联系
Bagging (bootstrap aggregating) Bagging即套袋法,其算法过程如下:
- 从原始样本集中抽取训练集.每轮从原始样本集中使用Bootstraping的方法抽取n个训练样本(在训练集中,有些样本可能被多次抽取到,而有些样本可能一次都没有被抽中).共进行k轮抽取,得到k个训练集.(k个训练集相互独立)
- 每次使用一个训练集得到一个模型,k个训练集共得到k个模型.(注:根据具体问题采用不同的分类或回归方法,如决策树、神经网络等)
- 对分类问题:将上步得到的k个模型采用投票的方式得到分类结果;对回归问题,计算上述模型的均值作为最后的结果.
Boosting Boosting是一族可将弱学习器提升为强学习器的算法. 关于Boosting的两个核心问题:
- 在每一轮如何改变训练数据的权值或概率分布? 通过提高那些在前一轮被弱分类器分错样例的权值,减小前一轮分对样本的权值,而误分的样本在后续受到更多的关注.
- 通过什么方式来组合弱分类器? 通过加法模型将弱分类器进行线性组合,比如AdaBoost通过加权多数表决的方式,即增大错误率小的分类器的权值,同时减小错误率较大的分类器的权值. 而提升树通过拟合残差的方式逐步减小残差,将每一步生成的模型叠加得到最终模型.
| Item | bagging | boosting |
|---|---|---|
| 样本选择 | 有放回抽取 | 总训练集 |
| 样例权重 | 均匀抽样 | 错误率越大权重越高 |
| 预测函数 | 每个预测函数权重相等 | 每个弱分类器有自己权重,误差小的分类器权重高 |
| 并行计算 | 可以并行 | 顺序,当前轮依赖前一轮结果 |
| 偏差-方差分解 | 降低方差(抑制过拟合) | 降低偏差(增强拟合能力) |
| 适应基分类器 | 复杂的(不剪枝决策树,神经网络) | 简单分类器 |
联系:都属于集成学习
判别模型和生成模型的区别
判别模型直接学习决策函数\(y = f(x)\)或者条件概率分布\(P(y \mid x)\)作为预测的模型,其基本思想是在有限的条件下建立判别模型,不考虑样本的生成模型,直接研究预测模型。例如k近邻,lr,svm,决策树等 生成模型由数据学习联合概率密度分布\(P(x,y)\),然后求出训练数据x的概率分布\(p(x)\),最后计算出后验概率 \(p(y \mid x) = p(x,y) / p(x)\),就是生成模型,例如朴素贝叶斯、隐马尔可夫模型、高斯混合模型、LDA、Restricted Boltzmann Machine
生成模型特点:是联合概率,首先需要从统计的角度分析数据分布情况,能够反映同类数据本身的相似度,不关心分类边界。 判别式模型特征:是条件概率,直接学习决策函数或者分布,不能反映数据本身的特征,寻找不同类别之间的最优分类面,反映不同数据之间差异,能够抽象问题,提取或者定义特征取简化学习问题。
例如让你判定一个人说话用的语言,生成式模型就是把所有语言都学习一遍,然后去判断,而判别式则不去学习,而是直接找语言模型之间的差别取分类。
联系:由生成模型可以得到判别模型,而判别模型不能得到生成模型。
机器学习评价指标
| 预测值\真实值 | 1 | 0 |
|---|---|---|
| 1 | TP | FP |
| 0 | FN | TN |
定义真阳率(召回率):\(TPR = \frac{TP}{TP+FN}\),表示正样本中被预测对的比率,当然这个比率越高越好
定义假阳率:\(FPR = \frac{FP}{TN+FP}\),表示负样本中被预测错的比率,这个比率越低越好
准确率:\(Precision = \frac{TP}{TP+FP}\),预测对的样本在所有预测为正样本中的比率
ROC 曲线就是横轴是假阳率,纵轴是真阳率。
而这个率跟分类阀值有关,不同的分类阀值假阳率和真阳率不同,而其下面的面积就表示AUC曲线。
AUC可以理解为我们随机从所有正样本随机选取一个样本,从所有负样本中选取一个样本,把这个正样本预测为正样本的概率为P1,把这个负样本预测为正样本的概率为P0,P1>P0的概率就是AUC,AUC本质反映分类器对样本的排序能力。
另一个常见的评价指标是KS(Kolmogorov-Smirnov),\(KS = max(TPR-FPR)\),反映模型的最优区分效果,比如推荐系统中这个指标较大比较好,我们要求更大的召回率比较好。而一些预测地震的模型可以要求准确率高。
常用激活函数
- sigmoid,一般放在最后一层,用来做预估结果计算,为0时结果为0,5,正数越大越接近1,负数越小越接近0(神经网络参数可能是负数所以最终结果会有负数),由于导数复杂度高中间层通常不用。
- tanh,常用在双塔的最后一层,为了是的输出最后一层的结果有正有负数,这样最后求dot后也是有正有负,则可以使用sigmoid,否则会最终结果都大于0.5,即预测样本结果为正。
- relu,最常用的,速度快,训练效率高,由于负数不激活,所以会导致节点死亡现象
- Leaky ReLU,负数的时候也传递,解决前面节点死亡问题
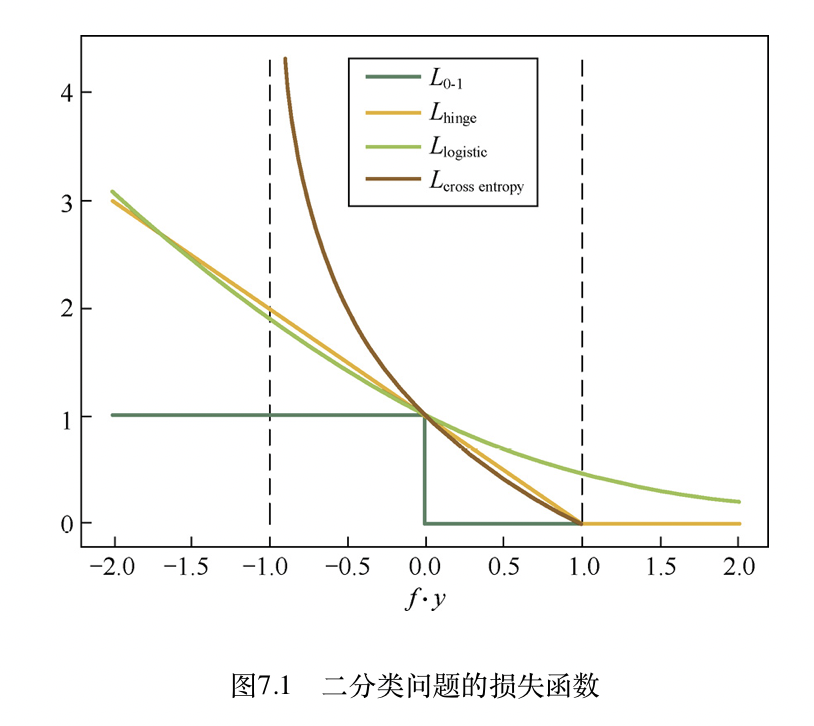
有监督分类常见损失函数
损失函数,本质是在使用数学方法评估两个数据分布的差异,其中y表示待学习样本本身数据分布,而f(x)表示模型学习到的数据分布,那么损失函数就是衡量这两个分布的接近程度,或者说差异程度。所以选择损失函数基本要对建模数据分布有个假设,二分类常用假设为二项(伯努利)分布,回归常用假设为正态(高斯)分布。
| 损失函数 | 定义 | 特性 | 常用算法 |
|---|---|---|---|
| 0-1损失 | \(L_{0,1}(y,f(x)) = 1:0 if (y ==f(x))\) | 非凸非光滑 | 感知机 |
| 绝对值损失 | \(L(y,f(x)) = abs(y - f(x))\) | 非凸非光滑 | |
| 感知机损失 | \(L_{p}(y,f(x)) = max(0, -y·f(x))\) | 非凸非光滑 | 感知器 |
| Log对数损失 | \(L_{log}(y,f(x)) =log_2(1+exp(-(f(x)·y)))\) | 光滑凸函数 | 逻辑回归 |
| Hinge损失 | \(L_{Hinge}(y,f(x)) = max(0, 1 - y·f(x))\) | 健壮性高 | 支持向量机SVM |
| 交叉熵损失 | \(L_{CrossEntropy}(y, f(x)) = -\sum_{i \in N}y_i · log f(x_i)\) | 光滑凸函数 | 逻辑回归及多分类 |
有监督回归常见损失函数
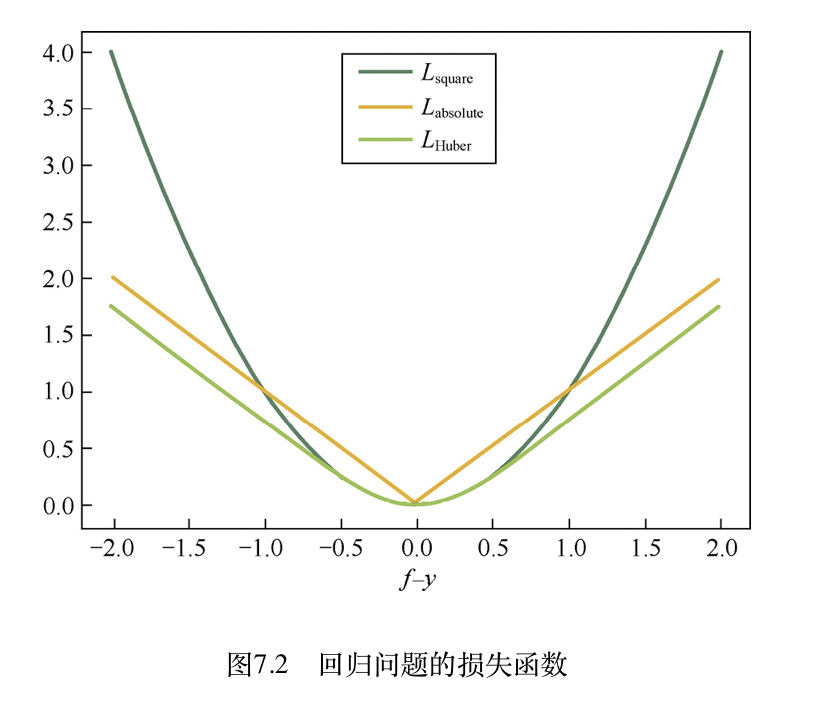
| 损失函数 | 定义 | 特性 | 常用算法 |
|---|---|---|---|
| 平方损失 | \(L_{square}(y, f(x)) = (y - f(x))^2\) | 光滑易优化,异常点敏感 | 线性回归 |
| 绝对值损失 | \(L_{absolute}(y, f(x)) = abs(y - f(x)\) | 非光滑,但异常点友好 |
还有一个是Huber损失,综合了前面两个函数的优点,公式为 \(L_{Huber}(y, f(x)) = \begin{cases} (f(x) - y)^2 & \text{abs(y - f(x)) <= \theta } \\ 2\theta\ abs(f(x) - y) - \theta^2 & \text{abs(y - f(x)) > \theta} \end{cases}\)
特征选择的方法
- Filter
- 包括方差选择法,如果特征方差为0,那么特征不发散,留着没有意义
- 相关系数法,特征对结果的影响系数,影响小的可以去掉
- 卡方检验,检查定性自变量对因变量的相关性
- 互信息法 求自变量和因变量的信息熵
- Wrapper,用类似搜索方法选择一些特征训练,然后在选择其他新的特征训练,选择最优特征
- Embedded 用l1正则化的特征稀疏型做特征选择
抑制过拟合的方法
- 增加样本数目
- 对数据做降维
- 选择简单的模型
- L1L2正则化
- eaery stop
决策树三种启发函数差异
| 简写 | ID3 | C4.5 | CART |
|---|---|---|---|
| 全称 | 最大信息增益 | 最大信息增益比 | 最大基尼系数 |
| 特性 | 倾向于取值多的特征 | 优化惩罚特征多结果 | |
| 变量类型 | 离散 | 离散&连续 | 离散&连续 |
| 模型类型 | 分类 | 分类 | 分类&回归 |
| 特征确实敏感性 | 敏感 | 不敏感 | 不敏感 |
| 分叉数目 | 多分叉 | 多分叉 | 二分叉 |
| 特征跨层级使用 | 不会 | 不会 | 会 |
| 是否建议剪枝 | 是 | 是 | 否 |
GBDT和xgboost区别
- 传统的GBDT是以CART作为基分类器,xgboost支持线性分类器
- GBDT优化用一阶导数,xgboost对代价函数进行了二阶泰勒展开,并且支持可导的任何自定义代价函数
- xgboost自定义了正则项,通过树的叶子节点数和节点权重,来防止过拟合
- shrinkage缩减,减小前面树的影响,给后面更大的学习空间,还支持列抽样,更大抑制过拟合
- 最优划分点算法
机器学习进阶
交叉熵损失和log损失的区别和联系
本质上它两是一个东西,一般在二分类问题中常叫log loss或logistic,而在多分类问题中经常叫交叉熵损失(Cross-entropy),证明见另一篇
tensorflow建模时常用的优化器有哪些
- tf.train.GradientDescentOptimizer,最基础的梯度下降,就一个参数学习率
- tf.train.MomentumOptimizer,基于动量的方法,每次梯度下降的时候除了考虑梯度之外,还会考虑之前下降的大小和方向,就好像有惯性一样,所以这里多了一个参数momentum,表示动量影响的大小,好处是遇到鞍点能走出来,收敛速度更快也更问题。
- Tf.train.AdagradOptimizer,自适应梯度下降,根据公式记录各个参数下降总和,运用模拟退火的思想,对下降多的控制后面少下降,下降少的后面多下降。多了一个参数initial_accumulator_value
- tf.train.AdamOptimizer,结合惯性保持和环境感知两个优点
工程工具类
spark中常见提升性能参数
- -num-executors 该参数用于设置Spark作业总共要用多少个Executor进程来执行,建议申请50-100
- executor-memory 该参数用于设置每个Executor进程的内存。每个Executor进程的内存设置4G~8G较为合适。
- executor-cores 该参数用于设置每个Executor进程的CPU core数量,Executor的CPU core数量设置为2~4个较为合适。
- driver-memory 参数用于设置Driver进程的内存。建议1G
- spark.default.parallelism 该参数用于设置每个stage的默认task数量。Spark作业的默认task数量为500~1000个较为合适。一般设置为num-executors * executor-cores的2~3倍较为合适,
- spark.storage.memoryFraction 该参数用于设置RDD持久化数据在Executor内存中能占的比例,默认是0.6。
- spark.shuffle.memoryFraction 该参数用于设置shuffle过程中一个task拉取到上个stage的task的输出后,进行聚合操作时能够使用的Executor内存的比例,默认是0.2。shuffle数据过大可调高
spark数据倾斜解决方法(参见美团文章)
- 过滤少数导致倾斜的key
- 提高shuffle操作的并行度
- 两阶段聚合(局部聚合+全局聚合)
- 采样倾斜key并分拆join操作
- 使用随机前缀和扩容RDD进行join