GBDT介绍
Gradient boosting Decision Tree算法是复合算法,前半部分Gradient boosting属于集成学习,迭代多个弱学习器,然后学习结果相加,最著名的boost算法是adaboost,其实总体思想和这个差不多,想了解可以看看之前的博客,而后半部分Decision Tree就是决策树了,著名的符号学派的经典算法。 目前在广告ctr预估方面用的很多的算法,当然推荐技术排序层也会用类似算法来提高点击率,其相对于基础的逻辑回归的优势在于能够自动选择特征,我们知道逻辑回归本身很强大,但是难点在于如何做特征工程,逻辑回归算法好不好主要决定于特征工程的质量,所以是一个目前相对很强势的算法。这个算法的工业实现最好的应该是陈天奇的xgboost了,有很多优化技术在里面,工业上很多都直接用这个训练。
| Item | GBTD | LR |
|---|---|---|
| 线性 | 非线性 | 线性 |
| 拟合能力 | 强 | 不强 |
| 特征选择 | 支持 | 手动 |
| 特征组合 | 支持 | 不支持 |
| 回归 | 支持 | 不支持 |
| 分类 | 支持 | 支持 |
| 多分类 | 支持 | 支持 |
| 输出概率 | 支持 | 支持 |
| 并行化 | 难度大 | 简单 |
算法框架
首先我们定义用f表示决策树,决策树在数学上本质可以认为是一个分段函数,我们用\(R_j\)表示分段空间,用\(b_j\)表示在这些空间上的实际函数值 那么对于决策树可以定义为f
\[f(x;\{R_j,b_j\}_1^J) = \sum_{j=1}^1b_j I (x \in R_j) \tag{1}\]有了单颗决策树,我们就可以定义GBDT树,其中K是总决策树数目
\[F = \sum_{i=0}^K {f_i} \tag{2}\]\(\mathcal{D} = \{(x_i, y_i)\}_i^N\),训练数据
目标函数\(\mathcal{L}\)定义为:
\[\mathcal{L} = \mathcal{L}(\{y_i, F(x_i)\}_1^N) = \sum_{i=1}^N{L(y_i,F(x_i)) + \sum_{k=1}^K{\Omega(f_k)}} \tag{3}\]公式前半部分是损失函数,可以用常用的平方损失或者logistic loss等,后面是正则化项,防止过拟合,而且对于GBDT来说每一颗决策树越简单越好,这样做一来训练简单,二来不容易过拟合

- 首先初始化\(f_0\),常见方法如随机或者用统计量初始化
- 正式训练过程
- 正常首先我们要计算残差\(r_i = (y_i , F_{k-1}(x_i)), i=1,2,...,n\),去拟合残差,但是当损失函数比较复杂时,我们用一个残差的近似值\(\tilde{y}_i\)代替,这里从整体要学到的gbd_tree \(F_N\)出发,当要计算当前\(f_k\)的时候,其残差可以用损失函数在上一点\(f_{k-1}\)处的偏导数代替,既整个函数\(F_N\)在当前\(f_{k-1}\)处的斜率就可以认为是损失函数梯度下降最快的点
- 正常这里用残差\(r_i\)去拟合一颗回归树,这里依然一样,得到第k棵树的叶节点区域\(R_j\)
- 利用线性搜索估计叶节点区域的值\(b_j\),使得损失函数极小化
- 更新回归树
计算优化
在算法1中,我们看到了有一个步长 \(\rho\),这个跟adaboost一样,是用来决定当前决策树对结果影响的权重的,等价于把决策树叶子节点的值放大了\(\rho\)倍,这里我们可以通过训练直接得到最终的值\(b_j\)。另一个问题是,这里求解的是损失函数的最小化,当这个问题不能直接求解的时候,我们转化为求解近似解的方法,这里通过在\(\rho\)处泰勒展开到二阶,得到近似后的解析解。 那么我们这里要求解的是\(f_k\),最小化目标函数为:
\[\begin{eqnarray*} \mathcal{L}_k & = & \sum_{i=1}^NL(y_i, F_{k-1}(x_i) + {\rho}f_k(x_i)) + \Omega(f_k) \\ & = & \sum_{i=1}^N L(y_i, F_{k-1} + {\rho}f_k) + \Omega(f_k) \\ & \thickapprox & \sum_{i=1}^N (L(y_i, F_{k-1}) + L^{'}(k-1)f(k) + \frac{1}{2}F^{''}(k-1)f_k^2) \\ & = & \sum_{i=1}^N (L(y_i, F_{k-1}) + \frac {\partial L(y_i, F_{k-1})} {\partial F_{k-1}} f_k + \frac{1}{2} \frac {\partial^2 L(y_i, F_{k-1})}{\partial F_{k-1}^2} f_k^2) + \Omega(f_k) \\ & = & \sum_{i=1}^N (L(y_i, F_{k-1}) + g_i f_k + \frac {1}{2} h_i f_k^2) + \Omega(f_k) \\ & = & \sum_{i=1}^N (L(y_i, F_{k-1}) + g_i \sum_{j=1}^J b_j + \frac{1}{2} h_i \sum_{j=1}^J b_j^2) + \Omega(f_k) \end{eqnarray*}\]其中GBDT最好的实现xgboost给出的正则化函数是
\[\Omega(f_k) = \frac{\gamma}{2} J + \frac{\lambda}{2} \sum_{j=1}^J b_j^2 \tag{4}\]其中\(\gamma\)和\(\lambda\)是正则化系数,J是叶子节点数目,\(b_j\)为当前叶子节点value
注意到上面第三步进行了二阶泰勒展开,把L函数看作一个整体做展开来求极小值,正常的二阶泰勒展开为:
\[f(x + \vartriangle x) \thickapprox f(x) + f^{'} \vartriangle x + \frac{1}{2} f^{''}(x) \vartriangle x^2\]整理出决策树相关的项:
\[\begin{eqnarray*} \mathcal{L}_k(\{R_j \}_1^J, \{b_j \}_1^J) & = & \sum_{i=1}^N \lgroup g_i \sum_{j=1}^J b_j + \frac{1}{2}h_i \sum_{j=1}^J b_j^2 \rgroup + \frac{\gamma}{2} J + \frac{\lambda}{2} \sum_{j=1}^J b_j^2 \\ & = & \sum_{x_i \in R_j} \lgroup g_i \sum_{j=1}^J b_j + \frac{1}{2}h_i \sum_{j=1}^J b_j^2 \rgroup + \frac{\gamma}{2} J + \frac{\lambda}{2} \sum_{j=1}^J b_j^2 \\ & = & \sum_{j=1}^J \lgroup \sum_{x_i \in R_j} g_i b_j + \sum_{x_i \in R_j}\frac{1}{2}h_i b_j^2 \rgroup + \frac{\gamma}{2} J + \frac{\lambda}{2} \sum_{j=1}^J b_j^2 \\ & = & \sum_{j=1}^J \lgroup \sum_{x_i \in R_j} g_i b_j + \frac{1}{2}(\sum_{x_i \in R_j}(h_i+ \lambda ))b_j^2 \rgroup + \frac{\gamma}{2} J \\ & = & \sum_{j=1}^J (G_jb_j + \frac{1}{2}(H_J + \lambda)b_j^2) + \frac{\gamma}{2} J \tag{5} \end{eqnarray*}\]上式中我们令
\[G_j = \sum_{x_i \in R_j}g_i\] \[H_j = \sum_{x_i \in R_j} h_i\]分析一下看看首先\(g_i, h_i\)是损失函数的一二阶导数,损失函数确定的时候,导数肯定也是确定的,导数中肯定有一项是\(F(K)\),这一项是随着训练轮数变化的,每一轮都会增加一个\(f_k\) 那么这两个式子的含义就是对于所有训练数据,\(x_i\)被划分到当前决策树k的叶子\(R_j\)中,满足当前条件的一介或者二阶导数的和,事实上xgboost所说的并行优化就是优化了这里
算法求解
有了上面推导,我们剩下的就是求解当前决策树k的划分\(R_j\)和划分后的值\(b_j\),首先,假设我们知道了树的划分\(R_j\),那么怎么求解\(b_j\)? 按照惯用方法,对公式5对\(b_j\)求导令导数为0,可得到
\[G_j + (H_j + \lambda)b_j = 0\] \[b_j^{*} = - \frac{G_j}{H_j + \lambda} \ \ j = 1,2,3,....,J \tag{6}\]带入导损失函数\(\mathcal{L}\)中,得到
\[\mathcal{L}_{k}^{*} = - \frac{1}{2} \sum_{j=1}^{J} \frac{G_j^2}{H_j + \lambda} + \frac{\gamma}{2}J \tag{7}\]所以说只要求解当前决策树的方法,那么剩下的就没有问题了,怎么分裂呢,首先我们肯定能想到就是枚举分裂点x,然后求解分裂后损失值是否降低,在xgboost中定义这样一个类似决策树Gain函数的公式
\[D = \frac{G_L^2}{H_L + \gamma} + \frac{G_R^2}{H_R + \gamma} - \frac {(G_L + G_R)^2}{H_L + H_R + \gamma} \tag{8}\]这里定义了树分叉成L和R之后的分数,分数用类似损失函数\(\mathcal{L}\)定义,上式的含义是(左子树分数 + 右子树分数 - 不分割得到分数) 另一点是发现算某个树分裂后的得分实际就是变化后的损失函数的相反数,所以得分越高损失函数越低,则分裂后效果更好。当然如果公式8小于0的话,不分裂比分裂要好,说明已经到叶子节点了。
样例 LSBoost
对于两个常见的损失函数,平方损失和Logit损失的时候我们如何计算 首先当损失函数是平方损失:
\[L = \frac{(y - F(x))^2}{2} \tag{9}\]在F处求导得到响应
\[y_i^{~} = -g_i = - \frac{\partial L(y_i, F(x_i))}{\partial F} = y - F(x) \tag{10}\]二阶导数为:
\[h_i = 1 \tag{11}\]那么就可以计算了,首先是树分裂算法


事实上树分裂的时候是在特征处做分裂的,我们运用贪心法每次枚举要当前树未分裂的特征,然后枚举分裂点,分裂函数计算分裂后是否更优,直到得到一颗满意的决策树,比如一个简单的例子:
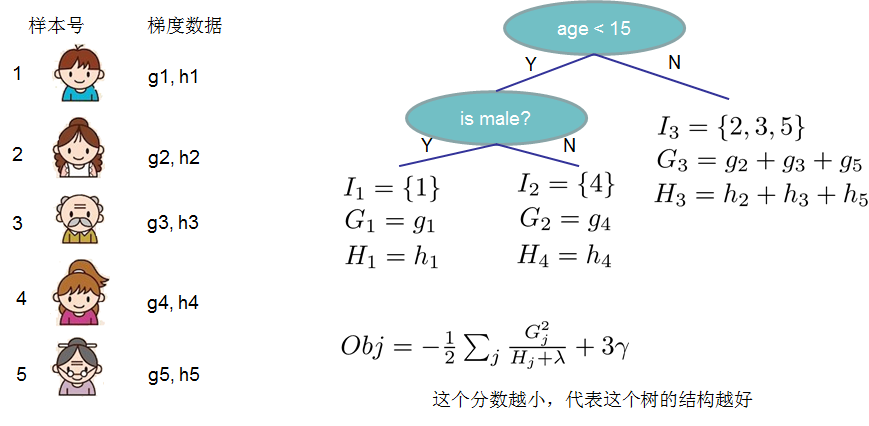
正则化
GBDT因为是不断拟合偏差的过程,所以Loss能够迅速下降,它是一个相对复杂的模型,所以是低偏差高方差,容易导致过拟合,就需要一些正则化方法
- 限制树的复杂度,正则化函数限制了数的节点数目和预测值的\(b_j\)的平方和都有惩罚,另外还可以把树的深度作为惩罚项
- 采样,每次只取部分样本训练
- 列采样,训练每一棵树的时候只取部分特征,引入随机森林的思想
- Shrinkage,进一步惩罚取值\(b_j\),乘以一个小于1的系数,让学习率降低
- Early stop,提前终止,并不一定需要所有的树,简单的有时候是比较好的