最大似然估计
最大似然估计(Maximum Likelihood Estimation),简称MLE,假设现在有个抛硬币机器,我们可以任意使用这个机器抛硬币后观测结果,假设只有两种情况,正面或者反面,假设抛硬币机器每次出的结果是服从某个已知分布的,而且每次出的结果都不受之前的结果的影响,即独立的,那么最大似然估计就是已经拿到观测结果,反推具有最大可能(概率最大)导致出现这个分布函数的参数。
是不是觉得这个过程很熟悉,这不就是机器学习建模的真实情况吗。确实是这样的,对于某个待优化场景,我们观测到了所有用户在这个场景的反馈样本,现在需要通过观测的结果去反推样本的分布,设计符合这个分布的模型,最终的目的是找到使得出现当前样本可能性最大的模型,去学习他的参数。从这个角度讲,所有的机器学习建模过程都可以叫做最大似然估计的过程,使用这个过程也可以推导出最基础的两个损失函数交叉熵损失和平方差损失。
交叉熵损失
做过机器模型应该都用过交叉熵损失,为什么他这么常用?来先看看它是个什么
信息量
熵的概念出自信息论,最基础的是信息量,信息量的定义公式
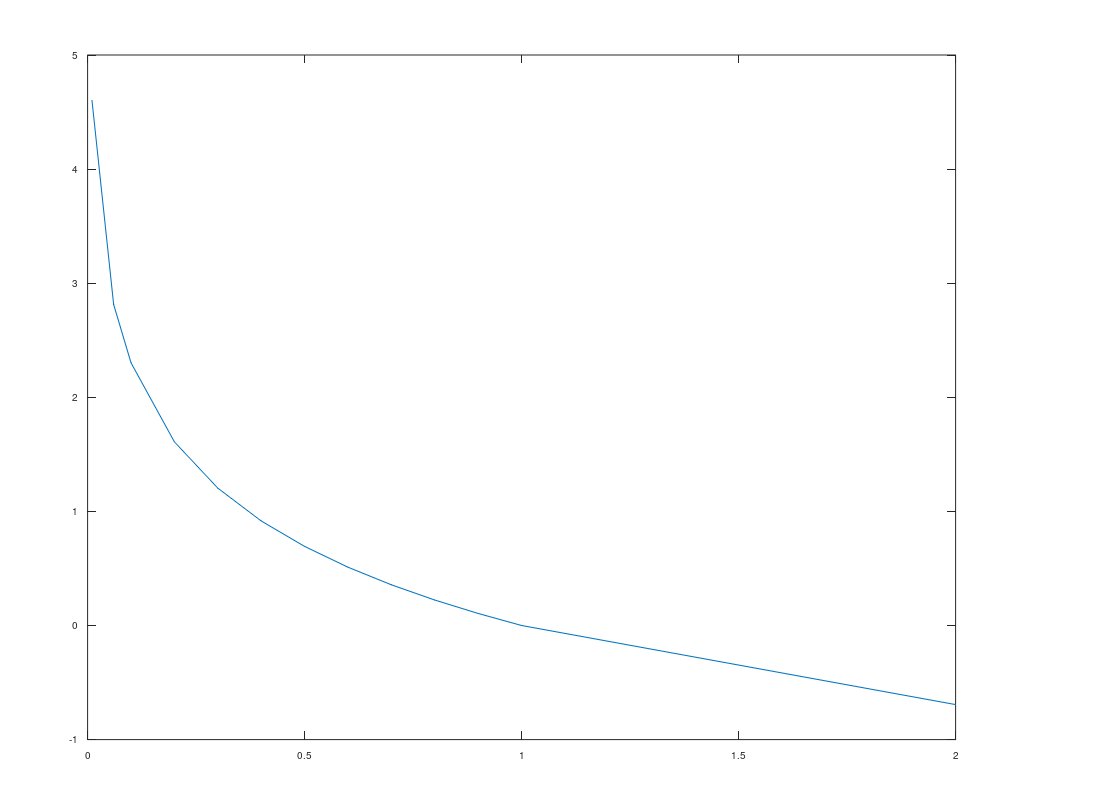
\[I(x) = -log(p(x))\]假设分布是离散分布,x为可能事件,p(x)为事件发生概率,信息量的函数如下,横轴是概率,纵轴表示信息量。
比如有两个事件:
事件A:巴西队入围了世界杯
事件B:中国队入围了世界杯
那个中包含的信息量多呢,当然是事件B嘛,因为事件B发生的概率太小了,从函数曲线也可以看出来,定义域在[0-1]之间,概率越小越接近0信息量越大,概率越大越接近1,信息量越小,这也符合实际情况。
熵
熵表示信息量的期望,公式为
\[H(x) = - \sum_{i=1}^n p(x_i)·log(p(x_i))\]还是上面的例子,比如事件A发生概率0.9,事件B发生概率0.1,则信息熵为
\[H(x) = 0.9 * -log(0.9) + 0.1 * -log(0.1) = 0.095 + 0.230 = 0.325\]相对熵
假设有两个相互独立的概率分布P(x)和Q(x),一般用KL散度(Kullback-Leibler (KL) divergence)来定义这两个分布的差异,KL散度的计算公式为:
\[D_{KL}(p \| q) = \sum_{i=1}^n p(x_i)·log(\frac{p(x_i)}{q(x_i)})\]其中n表示所有事件的个数
交叉熵
对上面公式做变形
\[D_{KL}(p \| q) = \sum_{i=1}^n p(x_i)·log(p(x_i)) - \sum_{i=1}^n p(x_i)·log(q(x_i))\] \[D_{KL}(p \| q) = -H(p(x)) + [-\sum_{i=1}^n p(x_i)·log(q(x_i))]\]可以看到前一部分就是概率分布P的熵,而后一部分就是交叉熵
\[H(p,q) = -\sum_{i=1}^n p(x_i)·log(q(x_i))\]对应到机器学习模型中,P表示观测到的实际分布,就是我们所谓的label,而Q模型预测出来的分布,就是所谓的predict score。其实本质是用KL散度来衡量预测分布和真实分布的差异,但是看前面公式会发现,化简后第一部分是分布P的熵,而P是实际分布是个固定的值,所以这部分可以忽略,也就是在机器学习问题中交叉熵等于KL散度,这也是为什么分类问题最常用用交叉熵做损失函数。
logistic损失和交叉熵损失
还记得学习逻辑回归的时候,逻辑回归使用最大似然估计得到的log损失,或者叫logistic损失。
\[\begin{eqnarray*} L_{log} & = & \prod_{i=1}^n P(y_i = 1 \vert x_i)^{y_i} · P(y_i = 0 \vert x_i)^{1 - y_i} \\ & = & log(\prod_{i=1}^n P(y_i = 1 \vert x_i)^{y_i} · P(y_i = 0 \vert x_i)^{1 - y_i}) \\ & = & \sum_{i=1}^n (y_i · log(f(x_i)) + (1-y_i)·log(1 - f(x_i))) \\ & = & \sum_{i=1}^n \sum_{j=1}^m y_{i,j} · log(f(x_{i,j})) \end{eqnarray*}\]前面化简过程这里不讲了,只看之后一步,因为log损失是二分类,所以如果把整个事件看成一个只有0,1的伯努利事件,m表示事件的可能性,这里为2,是不是抛掉最外层的求和,里面变成了一个公式。
其实本质上log损失和交叉熵损失是一个东西,或者一般把多分类叫做交叉熵损失,二分类叫做log损失,还有一个点是交叉熵损失前面有一个负号,所以使用交叉熵一般叫最小化交叉熵,而log损失叫最大化极大似然估计,只是差一个负号的问题。
交叉熵能否用于回归问题
我们知道回归问题常用平方差损失衡量,也可以从最大似然估计角度推导出来,有时间推导一下。
那么回归问题能用交叉熵做损失函数吗?这个问题最常出现在面试题目中和多目标优化中,在短视频多目标优化中假设有三个指标,点击率、完播率、播放时长,点击率很明显是二分类,而完播率是一个值,所以是个回归问题,而联合建模的时候会遇到一个问题,二分类的交叉熵损失和回归的mse损失分布差异很大,正常会遇到的是模型都学到回归模型这边去了。
我们实验,完播率是可以用交叉熵损失的,首先完播率本身分布在[0-1]之间,而且你用线上样本画个图的会发现他是U形的,横轴表示完播率,纵轴表示某个完播率下面的样本数目,即大多数样本是播放完成的或者没有播放的,而这恰好和二分类的分布很接近,即要么是1正常本,要么是0负样本。结合交叉熵公式,分布P中P(x)替换成真实完播率就可以。
那么除了这种分布很接近的之外,其他的比如视频时常这样的可以吗?答案是不可以,比如上面视频时长这样的,分布比较符合正太分布,还是用正常的MSE最好。
想想如果都反过来,比如分类问题用MSE,而回归结果用交叉熵,会发生什么问题?