现在客户运营已经离不开多目标了,原先做新闻推荐会关注单纯点击率,现在基本上会关注人均时长或者留存,都是围绕着多目标展开的。
多目标可以从两个维度分,第一个维度是多个目标前后有依赖关系,比如文章推荐或者商品购买推荐,都是有转化漏斗的,需要先点击才能发生阅读时长或者点赞,在商品上就是先点击后购买转化;另一种是前后目标没有依赖关系的,比如抖音沉浸式短视频,点击开就会播放视频,那么产生的指标例如点赞,评论播放时常都是没有先后依赖关系的,我们简称前一种是两阶段或者多阶段多目标优化,后一种为一阶段多目标优化。另一个维度是多目标的任务类型,比如GMV优化中点击率和转化率,都是二分类任务,而时常优化可能涉及点赞率和播放时常,就会有二分类和回归融合,后面我们简称为同类多目标和非同类多目标。这两个维度不同,在多目标模型设计阶段都需要针对性考虑设计。
MMOE模型是google在2018KDD上发布的,原文Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts。
模型简介
依然用我们上面的例子介绍,假设我们优化文章的阅读时长,假设时常只跟单个推荐文章的点击率和阅读时常有关,那么就相当于我们要从这两个指标入手建模。这是一个典型的两阶段、不同类融合多目标的任务。
现在深度模型基本围绕着模型结构和损失函数两块进行创新,MMOE主要是在结构部分的创新,同时它最后融合阶段使用集成学习思想。
模型结构创新
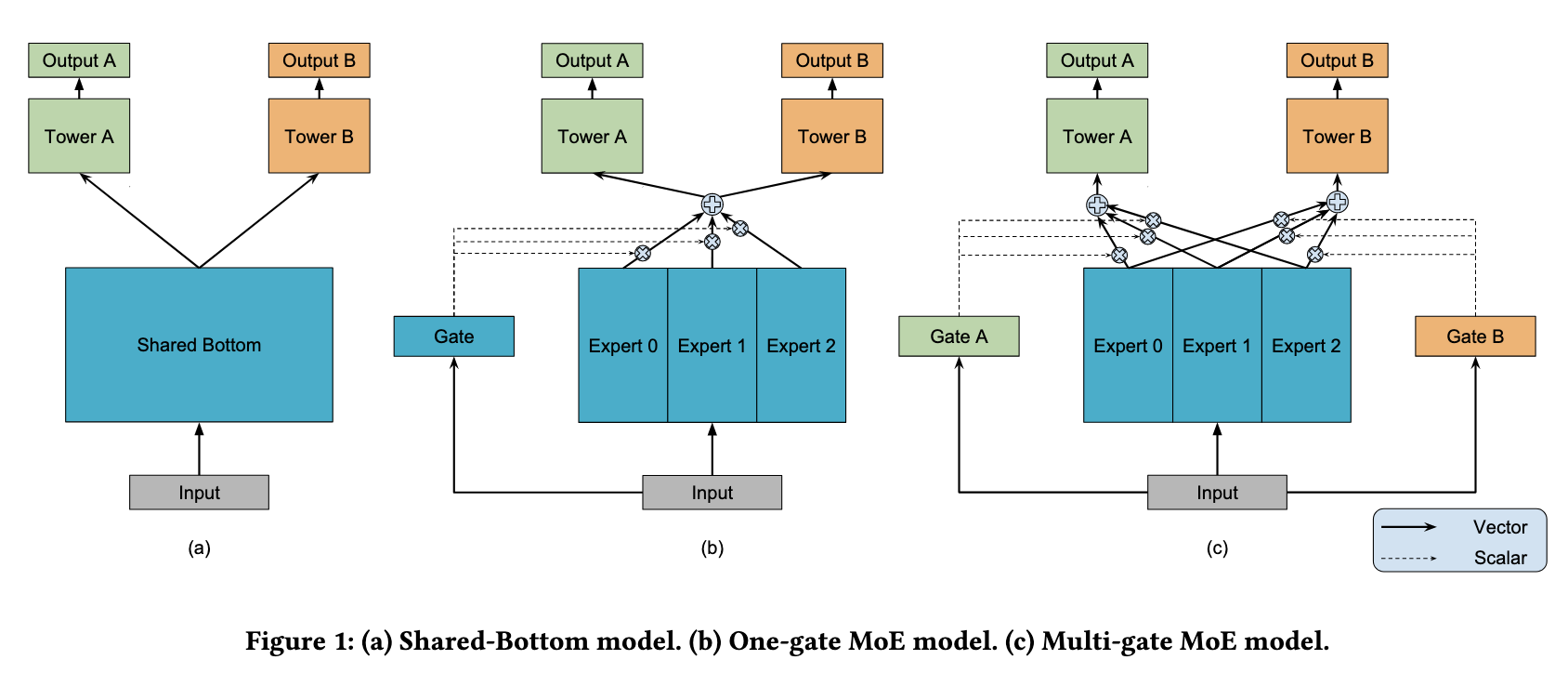
Shared-Bottom结构模型
模型结构层面,底层使用经典的Shared-Bottom结构,如下图a中所示,底层特征共享,一般分为categorical和numeric特征,前一类需要先做embedding稠密转化,后一类直接拼接就可以,接着使用全连接层学习,整个底层为共享网络。上层针对不同目标分别学习自己的网络,最后输出结果。
模型可以表示为\(y_k = h^k(f(x))\),其中k表示k个目标,f(x)表示底层模型,对应到图中底层Shared-Bottom,\(h^k\)表示第k个目标,为图中上面两个网络部分。
这样设计的好处是模型结构简单,参数少,问题是模型拟合能力不强,上层塔对拟合自己对应目标所需要的底层输入没有差异,如果上层学习两个任务差异性比较大则效果会很差。
MOE模型
针对上面问题就产生了下图b的MOE模型,主要解决上面说的拟合能力不强的问题,既然单个模型拟合能力弱,那能不能使用集成学习的思想,搞多个模型学习综合结果呢,MOE基本就是这个思路,每一个模型可以称作一个专家模型(Expert model),然后针对每个Expert产生的结果,需要加权综合,也就是Gate机制,给每个Expert学习出不同的权重,控制其对最终上层多个模型的影响。
表示为\(y_k = h^k (\sum_{i=1}^n g_i · f_i(x))\),其中i表示第i个Expert模型,然后每个模型又一个权重\(g_i\),其中\(\sum_{i=1}^n g_i = 1\)。
MMOE模型
上面模型创新点其实比较大,但是依然遗留下来一个问题加入上层多目标见差异比较大,或者说是类型两阶段或多阶段的多目标,则会效果比较差,MMOE给出的解决方案是,针对不同目标分别学习自己的Gate,事后想想这样才是合理的,而且也没有增加多少参数,如下面图c所示。
表示为\(y_k = h^k (\sum_{i=1}^n g_{i,k} · f_i(x))\),第i个Expert模型和对应的第k个目标,分别学习自己的Gate权重\(g_{i,k}\),其中对于每个目标\(\sum_{i=1}^n g_i = 1\)。
这里会涉及到Expert的数量,需要权衡模型复杂度和模型效果,找出合理的Expert数。
损失函数部分
损失函数这块,按照前面的同类任务多目标和异类任务多目标,同类比较简单,假设都是二分类任务,比如沉浸式短视频的点赞率和评论率的优化,假设使用交叉熵做损失函数。
\[L = \sum_{j=1}^K w_j · \sum_{i=1}^N L_{CrossEntropy}(y_i, f(x_i, \theta))\]其中K为目标的个数,\(w_j\)表是每个模型损失函数的权重,默认可以都为1,后面N表示样本数目,\(\theta\)表示模型参数。
对于异类多目标任务,比如视频播放时长和点赞率,一个分类一个回归任务,损失函数结果本身分布差异比较大,直接学习的话可能损失函数影响大的是回归模型,导致点赞学习不充分。一种是调低回归任务的损失函数权重,还有一种是对本身目标做一定的函数变换,比如log变换,但是总体在都是在想办法降低它的影响,没有从根本上解决问题。
另一个问题是对于多阶段目标的优化,比如文章点击率和阅读时常,涉及到两阶段,会遇到一个问题,没有点击的文章,时常应该怎么给,给0显然不是好的方案,可能是用户很喜欢的文章只是因为标题或者某些原因导致没有点击而已,这个在第二篇ESMM模型中会从根本上解决。
总结
模型的主要创新在模型结构上,使用了Gate机制和集成学习的思想,底层多个Expert学习多个模型,上层Gate控制学习自己的目标。
对于单阶段多目标比较友好,底层能够共享一些参数,模型复杂度也得到了控制。
最终多个目标线上要做融合,同样异类任务也会遇到分布一致的问题,融合一般有加权相加和次方乘法,不同分布建议用乘法,比如\(P_{ctr}^{\alpha} · P_{durtion}^{(1-\alpha)}\),可以使用离线grid-search学习最佳权重。
另外原论文介绍了两个现象:第一个是Shared-Bottom models的效果方差要明显大于基于MoE的方法,说明Shared-Bottom模型有很多偏差的局部最小点;第二个是如果任务相关度非常高,则OMoE和MMoE的效果近似,但是如果任务相关度很低,则OMoE的效果相对于MMoE明显下降,说明MMoE中的multi-gate的结构对于任务差异带来的冲突有一定的缓解作用。
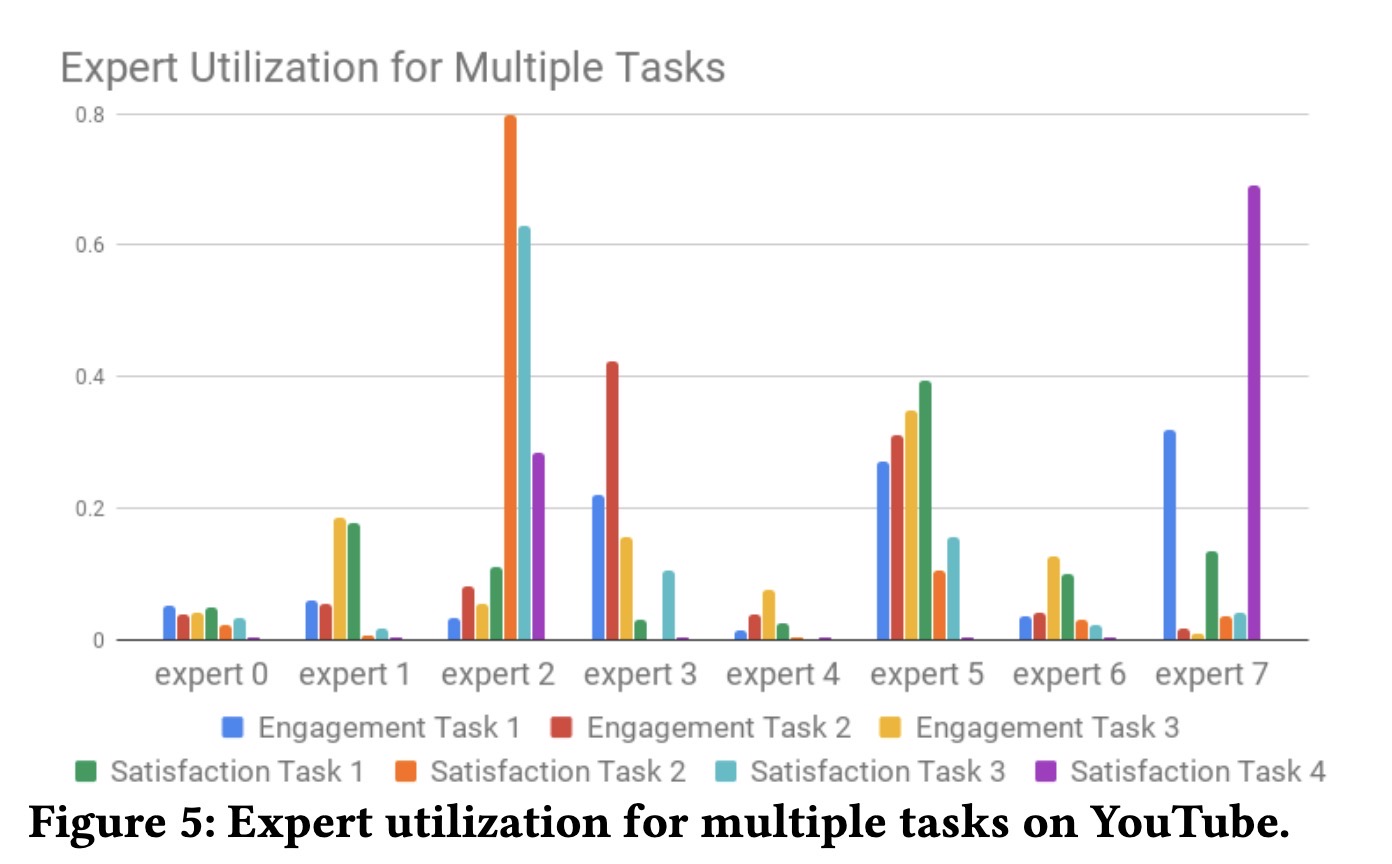
上图是youtube在2019recsys另一篇论文中分析他们各个expert对最终task的贡献权重,我们思考一个问题,使用这样多个expert通过集成学习的思路学习出来模型,每一个expert会对某个特定指标贡献度高嘛,以及它在模型更新或者重新训练后稳定的高的,如果不稳定的话应该怎么解决?
在Recsys 2020上腾讯提出了MMOE的改进PLE,对多个目标专有expert和模型深度的优化,并获得了最佳长篇论文,我们在这个系列第三篇讲。