word2vec是自然语言处理的最基础模型,他的embeding的思想也影响了很多其他比如推荐、广告等,是google的Mikolov大神团队2013年提出的,这里从我的理解的角度分析一下。
这篇文章主要是参考
简介
首先,为什么说他是一个经典模型,有两点原因,一个是因为他的的结果是每词的词向量,结果很灵活,比如我们计算两个词的相似度,以及后续衍生到段落的相似度,文章的相似度doc2vec,甚至是推荐中根据行为序列计算物品相似度。另一个是它是无监督的,可以直接用已有的文章训练不需要标注,并且计算效率很高,说白了就是使用的成本的低,这就让他能够大范围的研究及使用。
它的训练过程中,总体来说有两种思想,对应着网络的每次训练的输入输出,第一种就是根据上下文单词预测当前的单词,以及根据当前单词预测上下文单词。对应CBOW(Continuous Bag-of-Word)和SkipGram。
模型类似这样
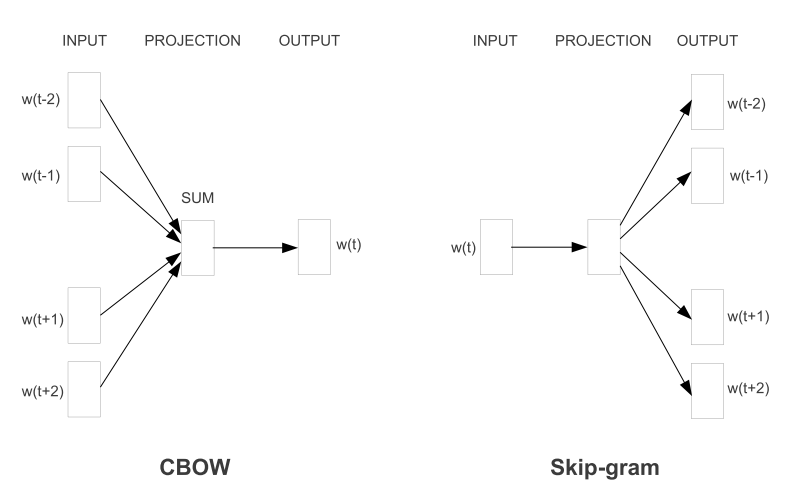
One-Word Model
最简化版本如下图,就是输入输出都只有一个词
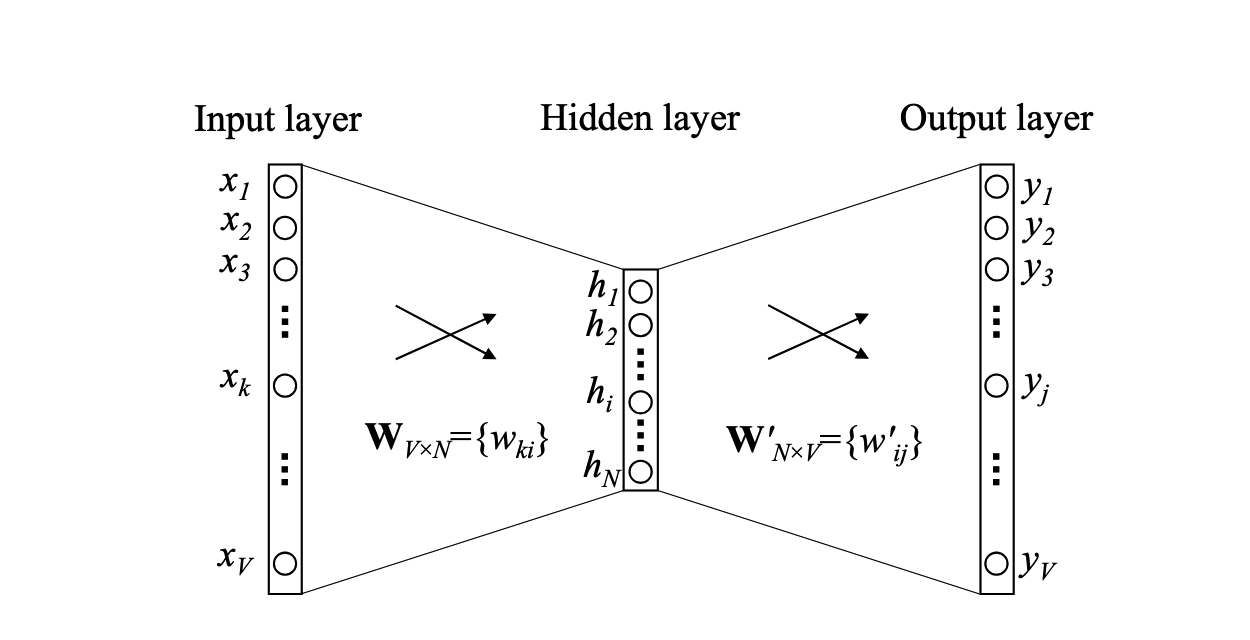
其中V表示词汇表的长度;N表示隐层神经元个数,也是最终词向量的维度,\(W_{V X N}\)表示输入层到隐层的权重矩阵,就是我们要学习的结果,每一行代表对应词的embedding。\(W_{NXV}^{'}\)表示隐层到输出层的权重矩阵,每一列也可以代表词向量
图中可以看到它是一个只有一个隐层的神经网络,输入和输出都是一个词向量,这个简单的模型其实就退化成自动编码机。
我们先讨论神经网络向前传播的过程,假设输入层表示为向量\(w_I\),是对单词进行one-hot后的结果,上图中\(x_1,x_2,x_3,...,x_V\)中只有\(x_k\)为1,其他位全部为0。那么它向隐层传播相当于取了W矩阵的第k行,也就是输入单词的的N维embeding向量,我们用\(V_{wI}\)表示
\[h = W^T \cdot X = v_{wI}^T\]考虑隐层h向输出层Y的传播,相当于是隐层1xN的矩阵和NxV的W’矩阵的乘积,得到一个1xV的结果向量。
\[u = h \cdot W'\]这里隐层相当于又相当于我们拿了W矩阵的第k行,我们用\(v_{k}\)表示,而计算的第i个Score相当于拿了W’矩阵的第i列,我们用\(v'_i\)表示,最终我们需要预测输出的是那个词,相当于一个多分类问题,所以这里我们使用softmax将结果u归一化到[0-1]之间,作为输出的概率
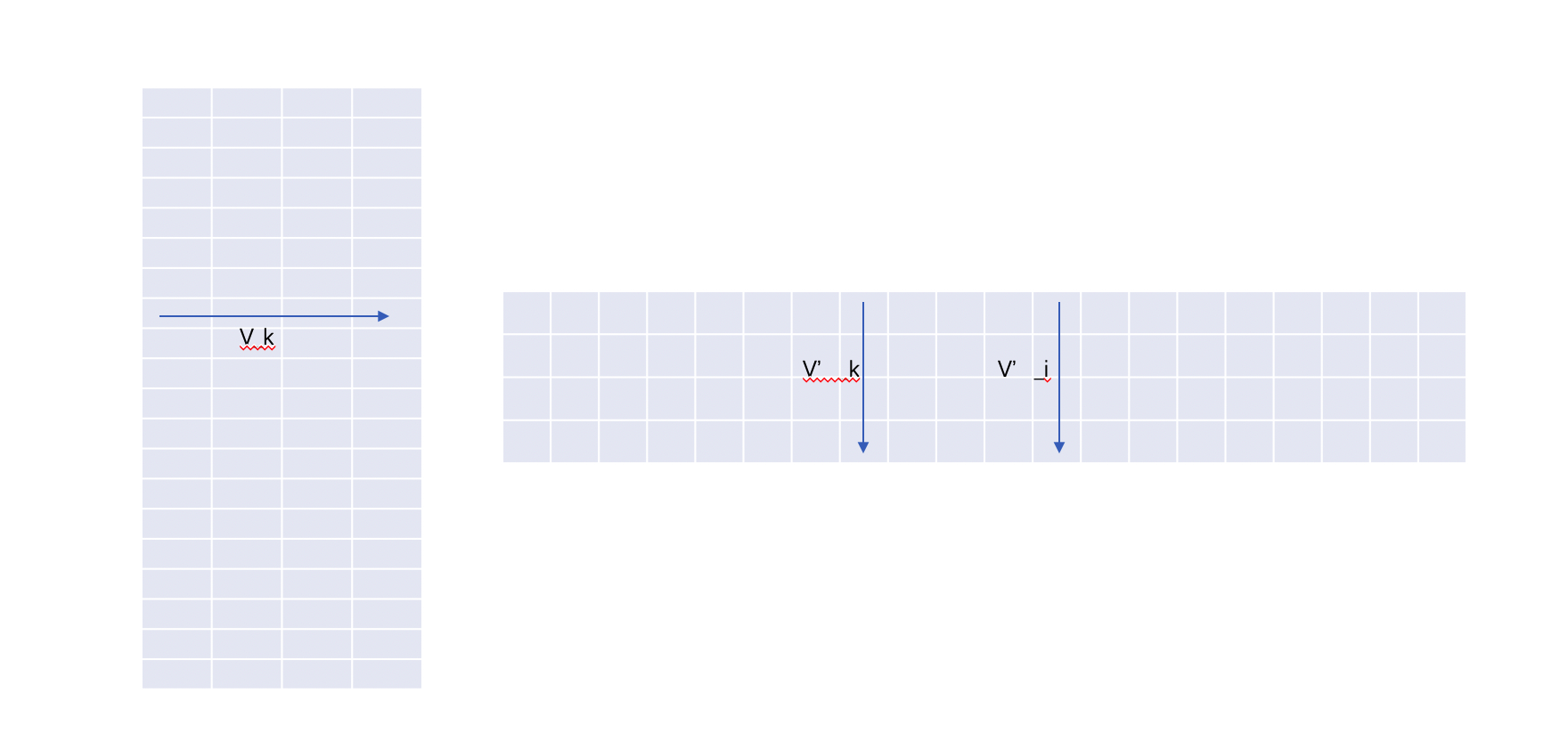
\[P(w_j|w_k) = y_j = \frac{exp(u_j)}{\sum_{i \in V} exp(u_i)} = \frac{exp(v'_j \cdot v_k)}{\sum_{i \in V} exp(v'_i \cdot v_k)}\]怎么理解这个过程呢,如下面矩阵表示图,第一个矩阵表示W,第二个矩阵W’,每一次训练相当于用W矩阵的第k行向量乘以W’矩阵的第k列矩阵,然后计算Score及反向传播。等到预估的时候,相当于用W的第k行和W’矩阵的每一列分别计算score,然后经过softmax判断那个概率最大,这个过程计算量比较大,后续我们说它的优化方法。
模型训练
因为输出层是softmax结果,所以我们用损失函数用最大似然接球,目标函数为
\[O = max P(w_O | w_I) = max log(\frac{exp(u_j)}{\sum(u_k)}) = max (u_j - \sum_{k=1}^V exp(u_k))\]按照惯例我们转换一下求最小值,则损失函数
\[E = -u_j + log \sum_{k=1}^V exp(u_k)\]对w求导数得到
\[\frac{\partial{E}}{\partial{w'_{ij}}} = \frac{\partial{E}}{\partial{u_j}} \cdot \frac{\partial{u_j}}{\partial{w'_{ij}}} = (y_j-t_j) h_i\]这里\(y_j\)是预估值,\(t_j\)是真实值,而\(h_i\)是隐层的第i项。
所以梯度下降更新公式为
\[w'_{i,j} = w'_{i,j}(old) - \eta (y_j-t_j)h_i\]上面是W’矩阵的更新函数,接着我们看从输入到隐层的W矩阵的更新,继续反向传播,输出层的V个神经元都会影响隐层h
\[\frac{\partial{E}}{\partial{h_i}} = \sum_{j=1}^{V} \frac{\partial{E}}{\partial{u_j}} \cdot \frac{\partial{u_j}}{\partial{h_i}} = \sum_{j=1}^V(y_j - t_j) w'_{i,j} = W'_i \cdot P\]其中\(W'_i\)时W’的第i行,\(P = {y_j - t_j \mid j = 1,2,3,...,V}\),所以更新公式为
\[v_{wI}^T = v_{wI}^T - \eta W' \cdot P\]到这里,完整的反向传播就结束了,我们看出,这里的主要计算量是在从隐层到输出层的更新,因为每一个训练样本需要更新一次W’矩阵,这个计算量是NxV的,是比较大的,后面专门有个针对这一块的优化思路。
CBOW model
首先图的模型如下
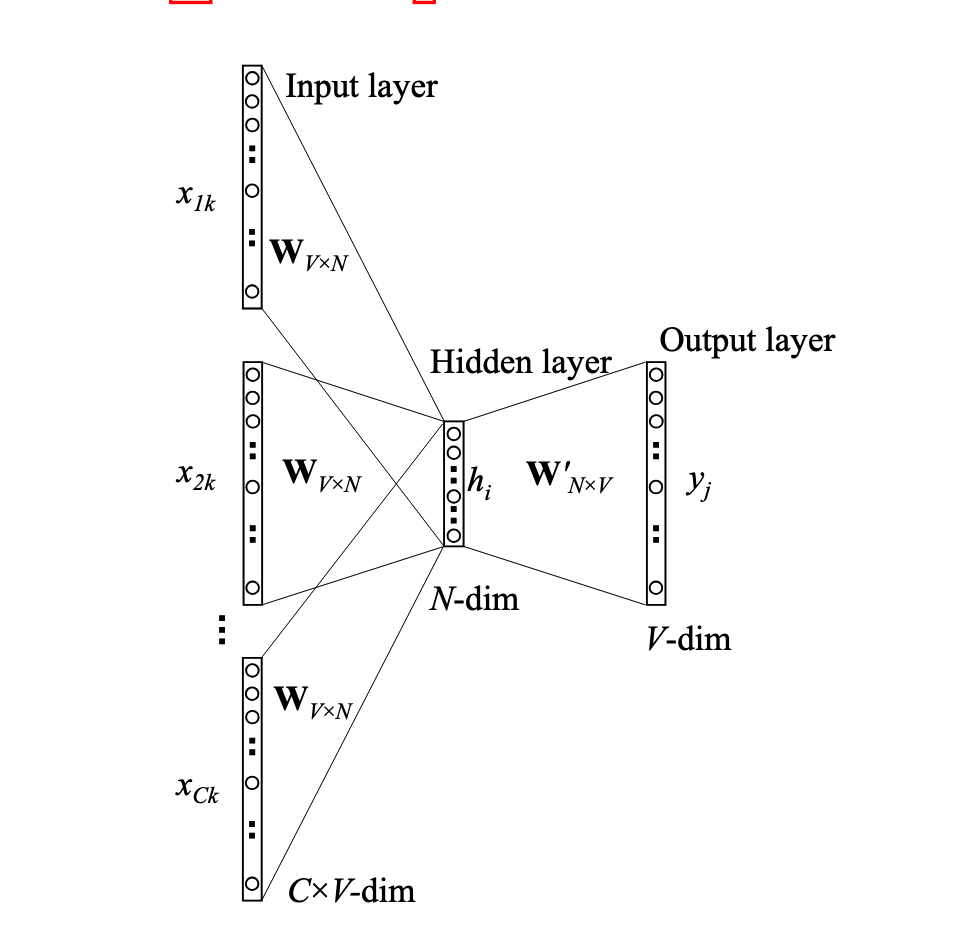
不同点是,这里思路是根据单词的上下文预测当前单词,这里有个窗口的概念,比如窗口是5的话,就是当前单词的前面两个和后面两个,所以这样,输入就变成了多个单词了,假设单词数量为C,则输入到隐层矩阵的更新为
\[h = \frac{1}{C} W^T(x_1 + x_2 + ... + x_C) = \frac{1}{C} (v_{w1} + v_{w2} + ... + v_{wc})^T\]后面的更新就一样了,另外就是反向传播的时候,原来是隐层到输入层更新W的时候,只更新这个词对应的一行,现在有多个词,更新的时候讲h的梯度均摊到每一个词上,更新公式为
\[v_{wI,c}^T = v_{wI,c}^T - \frac{1}{C} \eta W' \cdot P, c = 1,2,...,C\]SkipGram Model
另一种就是根据当前单词预估起单词上下文的训练模式,这样相当于输出层有多个值,就不是一个多项分布,而是C个多项分布,模型图如下
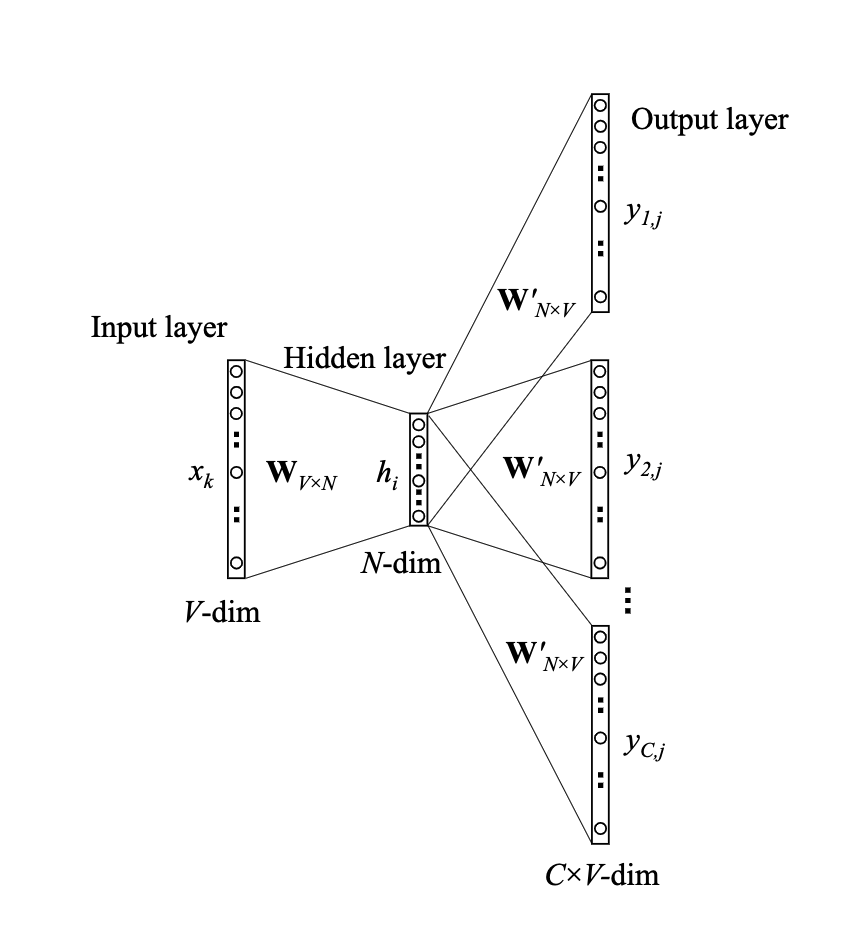
首先,前面输入到隐层不变,但是隐层到输出层因为变成了多个输出,所以最终softmax也变为C个
\[P(W_{c,j} | W_I) = y_{c,j} = \frac{exp({u_{c,j}})} {\sum_{k=1}^V exp(u_{c,k})}, c = 1,2,...,C\]另外u的计算也是和之前一样,其中W’是一个共享矩阵,隐层肯定是一定的,W’又是共享的,所以最终计算出来输出矩阵就是一个矩阵,只是这个模型没有预测的过程,训练后的参数就是我们要的结果,所以我们能够保证训练时更新多次保证把参数矩阵更新到就好了
下面我们看SG反向传播的部分,跟前面稍有不同,损失函数为:
\[\begin{eqnarray*} E & = & - log P(w_1,w_2,...,w_C| w_i) \\ & = & -log \prod_{c=1}^C p(w_c | w_i) \\ & = & -log \prod_{c=1}^C \frac{exp(u_{c,j})}{\sum_{k=1}^V exp(u_{c,k})} \\ & = & -\sum_{c=1}^C u_{j,c} + C \cdot log \sum_{k=1}^V exp(u_k) \end{eqnarray*}\]对它求导
\[\frac{\partial{E}}{\partial{w'_{i,j}}} = \sum_{c=1}^C \frac{\partial{E}}{\partial{w'_{c,j}}} \cdot \frac{\partial{u_{c,j}}}{\partial{w'_{i,j}}} = \sum_{c=1}^C (y_{c,j} - t_{c,j}) h_i = Q_j \cdot h_i\]有了梯度,我们可以用梯度下降更新
\[w'_{i,j} = w'_{i,j}(old) - \eta Q_j h_i\]接着是对隐层的梯度
\[\begin{eqnarray*} \frac{\partial{E}}{partial{h_i}} = \sum_{c=1}^C \sum_{j=1}^V \frac{\partial{E}}{\partial{u_{c,j}}} \frac{\partial{u_{c,j}}}{\partial_{h_i}} \\ & = & \sum_{c=1}^C \sum_{j=1}^V (y_{c,j} - t_{c,j}) w'_{i,j} \\ & = & \sum_{j=1}^V Q_j w'_{i,j} = W'_i \cdot Q \end{eqnarray*}\]如之前讲的,隐层相当于是拿到W矩阵中的第I行,所以每次只需要更新一行
\[v_{wI}^T = v_{wI}^T(old) - \eta W' \cdot Q\]Hierarchical SoftMax
算法讲完了,基本上就是这样,但是我们也看到了,不管是CBOW还是SG模型,对于每一个训练样本,都需要更新W’整个矩阵的梯度,假设有P个训练样本,复杂度就是P * N * V,我们知道V本身就很大,所以这个复杂度的训练成本是很高的。
其实考虑一下,计算量大的部分都是在W’这个矩阵上,或者换句话说是从隐层到输出层上,所以word2vec使用了两种优化策略,Hierarchical Softmax 和 Negative Sampling,两个方法的思想都一样,就是不在完全更新W’,其中Hierarchical Softmax是对Softmax为输出的所有模型的通用方法,其本质是优化Softmax的分母的求和,让他变成一个log复杂度的树。
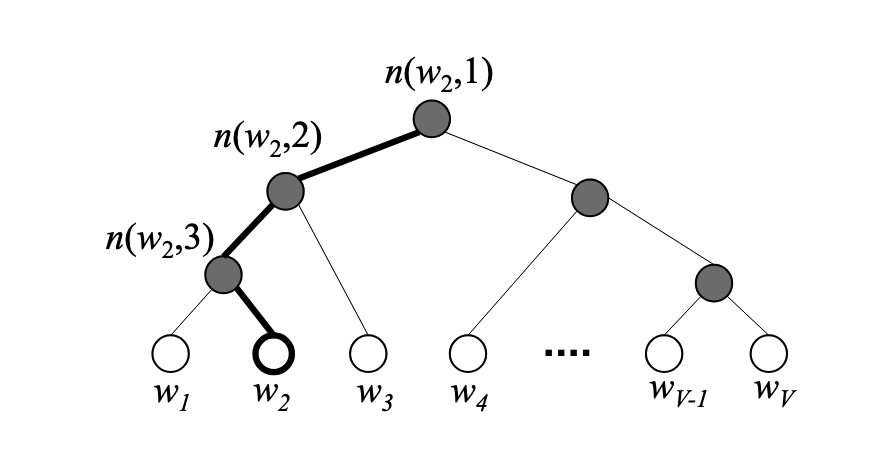
如上图,其中的叶子节点表示词汇表中的V个词,黑色的是非叶子结点,其中保存一个和隐层维度相等的一个向量,使用一个sigmod函数:\(\sigma = \frac{}{1}{1 + exp(-x)}\),判断当前节点是该向左还是向右,目标是从root节点到叶子结点找到一条路径,使得\(w = w_O\)的概率最大。在每一个节点定义
\[P(n, left) = \sigma (v'_w \cdot h)\] \[P(n,right) = 1 - \sigma(v'_w \cdot h) = \sigma(-v_w' \cdot h)\]定义概率
\[P(w = w_O|w_I) = \prod_{j=1}^{L(w)-1} P(\sigma(I(n(w,j+1 == left)v'_w \cdot h)))\]其中I()是只是函数,条件成立为1,否则-1,L(w)表示路径的长度,计算的是从跟节点到叶子节点的概率。训练的时候只需要更新节点的参数\(v'_w\)就好了。
这里因为在非叶子节点向左和向右的概率和为1,所以分裂下去,最终叶子节点的总和也为1,可以得到
\[\sum_{j=1}^V p(w_j = w_O) = 1\]在反向传播的时候,损失函数为
\[E = -log P(w = w_O | w_I) = -\sum_{j=1}^{L(w)-1} log \sigma ([I]v'_j h)\]这里用[I]表示前面的指示函数\(I(n(w,j+1)==left)\),用\(v'_j\)表示\(v'_{m(w,j)}\)
之后逐项求梯度
\[\frac{\partial{E}}{\partial{v'_j h}} = (\partial([I]v'_j h))[I]\]然后对[I]分情况讨论,如下式,如果[I] = 1,那么\(t_j = 1\),否则\(t_j = 0\),这个公式和前面类似,就是预测值和真实值的差。
\[\frac{\partial{E}}{\partial{v'_j h}} = \partial(v'_j h) - t_j\]那么我们就可以求出对参数\(v'\)的梯度了
\[\frac{\partial{E}}{\partial{v'_j}} = \frac{\partial{E}}{\partial{v'_j h}} \cdot \frac{\partial{v'_j h}}{\partial{v'_j}} = (\partial(v'_j h) - t_j) h\]那么就可以进行梯度下降了
\[v'_j = v'_j(old) - \eta (\partial(v'_j h) - t_j)h,j=1,2,3,...,L(w)-1\]然后考虑对隐层h的梯度
\[\frac{\partial{E}}{\partial{h}} = \sum_{j=1}^{L(w)-1} \frac{\partial{E}}{\partial{v'_j h}} \cdot \frac{\partial{v'_j h}}{\partial{h}} = \sum_{j=1}^{L(w)-1}(\partial(v'_j h) - t_j) \cdot v'_j\]可见,经过这样,我们把原先的复杂度中最大的V部分优化为了log(n)
还有一种优化方法,同样也是最隐层到输出层矩阵更新的优化,叫Negative Sampling,其思想是每一个训练数据来的时候,对要更新的负例做采样,这里正例就是输出结果对于的矩阵列,其他都是负例,采样的时候可以根据词频进行采样,详细方法方法这里不说了。