Recommendation bryond Matrix Factorization

摘要

在过去的十年中，矩阵分解已经得到了广泛的研究，并已成为最受欢迎的个性化推荐技术之一。然而，基于矩阵分解的推荐模型中采用的点积不满足不等性，这可能会限制它们的表达性并导致次优解。为了克服这个问题，我们提出了一种称为度量分解的新型推荐技术。我们假设用户和物品可以放置在低维空间中，并且可以使用满足不等式属性的欧几里德距离来测量它们的明确相似度。为了证明其有效性，我们进一步设计了两种度量分解变量，一种用于评分预估，另一种用于个性化项目排序。对许多真实世界数据集进行的大量实验表明，我们的方法在评级预测和项目排名任务方面都大大优于现有的最新技术水平。

介绍

从用户评分矩阵中学习低阶潜在结构构成了数十年推荐系统研究的基石[14,19,28,32]。这个被广泛称为矩阵分解[28]的概念已经成为更受欢迎的推荐技术之一。凭借其简洁性和有效性，这一系列技术已经取得了不可思议的成功，并在NetFlix比赛等著名竞赛中获得了成功并取得了广泛的应用。

另一方面，从优势方面来说，基于矩阵分解后的空间向量不仅计算简单，而且效率极高。但是它有个很明显的缺陷就是分解后计算相似度不满足三角不等式，这种计算的传递性对于捕捉用户和物品之间的相似性非常重要。为此，基于欧几里德距离作为相似度的度量学习方法一直被认为更加娴熟和富有表现力。

本文主要关注两种范式的桥接。首次，我们探索了“解开度量向量空间”的概念，即通过因子化学习度量空间中的低秩结构。为此，我们提出的方法，分解度量学习（FML）可以被解释为包括距离而不是评级分数的因子化偏好矩阵。这很容易与标准矩阵因子分解不同，后者通常通过评级得分对用户项目相似性进行编码

我们的方法背后的主要动力是结合两种方法中最好的一个，从而减轻每种分解的固有弱点。更具体地说，MF算法效果受限于简单的点积计算。众所周知，点积不满足三角不等式[25] 2，限制了矩阵分解的表达性，因此导致了次优解。详细的解释可以在[13,15]中找到。此外，实验研究还表明，矩阵分解对于大的潜在向量有过拟合风险，这大大限制了模型的可行性和能力[13,42]。

度量学习的最近推广算法协同度量学习（Collaborative Metric Learning）已经证明能够解决这个问题。然而，它自己本身拥有一系列问题，即向量空间中的过度拥塞[37]。虽然它学习了相似性聚类，但我们假设学习聚类也可能因过度拥塞而受到影响，从而导致次优解。我们在定性实验中进一步证明了这一现象。

为了缓解上述问题，我们提出了一种新颖的技术：分解度量学习（FML）。关键的直觉是首先将偏好转换为距离然后用欧几里德距离替换点积。FML从位置和距离的角度考虑推荐问题，并直接将距离矩阵分解为用户和项目的隐式向量，它不仅可以避免上述缺点，而且还适用于评分预估和物品打分。都是根据估计的空间距离进行的。因此，这可以解释为通过分解来embedding到空间距离。总而言之，这项工作的主要贡献总结如下：

我们提出了一种新颖的技术，即分解度量学习（FML），其中我们探索了在度量向量空间中建立低秩结构的概念。在我们的方法中，用户和物品被表示为多维坐标系统中的点（即，欧氏向量空间）。建议基于用户和物品的相似度，在欧式空间中定义。然而，与其他度量学习方法不同，我们的创新在于把评分矩阵分解到欧式空间中。
我们指定两种FML变体来解决两个经典且完善的推荐任务：评分预估和物品打分。我们的模型可以有效地学习到用户和物品在空间中的位置。
在大规模标准公开数据集上进行的实验表明，我们的模型在评分预估和物品打分方面都大大超过了最先进的模型。这表明我们的简单且效果优秀。

背景

建议的方法

在本节中，我们将介绍我们的分解度量学习方法。图1说明了FML的简要概述。假设我们有M个user和N个item，偏好（评分或隐性评分）矩阵表示$R∈R^{M×N}$。$R_{ui}$的值表示用户u对物品i的偏好,评分矩阵R可以是明确的评分，例如显示评分或隐式反馈。显式可以用于待推荐物品的预估打分，而隐式反馈通常用于个性化排名。这两个任务在推荐区域是常见的，所以不要夸大它们[27]。

简化FML的简化说明。它主要有两个步骤：首先，通过过程1转换偏好矩阵（评级或交互）的距离矩阵。其次，将距离矩阵分解为度量向量空间中的用户和物品的空间位置

偏好作为距离

我们的目标是解开度量向量空间，以通过分解来学习用户和物品。矩阵分解通过将偏好矩阵（从显式/隐式反馈）分解为点积来学习用户和潜在因素。偏好矩阵也可以视为相似矩阵。由于相似性和距离是两个相反的概念，我们需要将用户偏好转换为第一个距离。

在这里，我们给出了一个简单而有效的公式，距离计算通过下面公式：

\[Distance(u,i) = Max Simlarity - Similarity(u,i) \tag{1}\]

Max Simlarity是矩阵中的最大评分值，比如上面样例中的5。通过这个转换，我们把喜好程度转换为距离，同时保持了其分布。这个转换可以应用于显式和隐式反馈。距离是空间上可以计算的。并且距离函数满足四个关键条件：非负性，唯一性，对称性和满足三角形不等式[40,43]。在不同的应用领域中使用了许多距离函数，例如离散距离，欧几里德距离，图距离。在欧几里德空间$R^k$中，两点之间的距离通常通过欧几里德距离（或l2范数距离）来测量。由于其简单的形状和有用的特性，它已广泛应用于机器学习，传感器网络，几何，人脸识别等[3,8,22]。在实践中，通常采用平方欧几里得距离来避免计算方根的麻烦。

假设用户和物品在度量向量空间中的位置通过$P_u∈R^k$ 和 $Q_i∈R^k$表示，这里我理解$P_u$表示用户u在空间中的表示，而$Q_i$表示物品i在欧几里得空间中的表示。我们使用平方欧几里德距离测量用户和物品之间的距离：

\[D(u,i) = {||P_u - Q_i||}_2^2 \tag{2}\]

图1简单地说明了FML的过程。首先，我们通过等式1从偏好矩阵得到距离矩阵，然后我们将距离矩阵分解得到用户和物品的空间位置。之后，如果需要，我们可以轻松通过计算回复偏好矩阵中的每一个值然后去做推荐。

因式分解距离矩阵做物品打分

当只有隐式反馈时，个性化打分是推荐系统中的一项重要任务。在许多现实世界的应用程序中，隐式数据（如购买记录，展示和点击）比显示评分更容易获得，这导致将隐式反馈建模为主要焦点。我们遵循以前的研究，并将隐式反馈定义为二元值，其中正向反馈为1，其他情况为0 [13,18]。

首先，我们使用以下公式将隐式反馈转换为距离

\[Y_{ui} = a * (1 - R_{ui}) \tag{3}\]

由于$R_{ui}$等于0或1，因此假如$R_{ui} = 0$的时候距离$Y_{ui}=a$，如果$R_{ui}=1$的话距离$Y_{ui}=0$，因此控制用户和物品距离非常灵活。

对于ranking任务，考虑到展示而没有点击等这些通常是有益的[13,16]。例如，通过对展示和点击的采样，以成对方式训练贝叶斯个性化排名和协作性网络学习。WRMF和NeuMF采用point wise学习方法，但也考虑负向物品。在这项工作中，采用point wise，因为我们希望直接将距离分解为用户和物品的embeddings。

\[\mathcal{L}(P,Q) = \sum_{(u,i)\in{R}} c_{ui}(Y_{ui} - \mathcal{D}(u,i))^2 \tag{4}\]

在这里，所有未观察到的相互作用都被定位为置信度$c_{ui}$。它的计算方式为：$c_{ui} = 1 + \alpha w_{ui}$，其中$w_{ui}$表示隐式反馈的次数，例如，如果用户浏览项目两次，那么$w_{ui}$ = 2。对于表达大字数，可以通过log变换[16]。由于此信息通常存在于公开可用的数据集中，因此我们令$w=R_{ui}$（0或1）。正则策略将在3.4节中介绍。即使我们采用point wise方案，这样能够使得用户喜欢的物品在空间中离当前用户更近，而且能够是用户不喜欢的在空间距离中更远。与大多数基于度量学习的模型不同，这种模型通过某些强制策略用户特别偏爱的物品距离更远，这种方法中的控制机制为未知物品进入用户区域提供了可能性，这对于推荐任务来说是非常必要的。可以作为一个过滤器从未知待推荐物品中选择物品进行推荐。我们模型的另一个重要特征是它可以间接地聚类有共同喜好物品的用户群。这个属性可以捕捉邻居之间的关系，这也是物品推荐的重要因素[1]。

因式分解距离矩阵做评分预估

如前所述，我们的方法也可以应用于评分预估。对于评分预估，仅考虑观察到的行为数据就足够且更有效。让$\mathcal{K}$表示观察到的行为数据集。首先，我们将评分矩阵R通过下面公式做一次变换：

\[Y_{ui} = R^{max} - R_{ui} \tag{5}\]

这里$R^{max}$表示最高评分。如果$R^{max}$ = 5且评分为3，则距离$Y_{ui}$ = 5 - 3 = 2。

与矩阵分解相同[19]，一些潜在的因素对结果也很重要。例如，某些项目往往会收到更高的评价;一些用户倾向于给予低评分。因此，我们将全球用户和物品偏差条款整合到我们的评估估算方法中。最终得分公式如下：

\[\hat{Y} = \mathcal{D}(u,i) + b_u + b_i + \mu \tag{6}\]

这里，$\hat{Y}$表示预测距离。比较分别是用户和偏差项;μ是全局偏差，等于从训练数据构造的主题距离。通常，我们可以添加超参数τ以将μ缩放到更合适的值。

我们要考虑的另一个重要方面是评分数据的可靠性和稳定性。大多数评分预估算法忽略了评分的噪声，并假设所有评分都是真实可靠的。尽管如此，并非所有观察到的评分都具有相同的权重[19]。例如，一些用户在被要求在不同时间两次对同一项目进行评分时可能会给出两个不同的分数[17]。以前的研究[2,17]表明极端化（例如1和5）比中等等级（例如2,3和4）更可靠。为了缓解这种情况，我们建议为每个评分得分添加一个相关值，并获得以下损失函数

\[\mathcal{L} = \sum_{u,i\in \mathcal{K}} c_{ui}(Y_{ui} - \hat{Y}) \tag{7}\]

需要注意得是置信度$c_{ui}$可以表示许多因素。受[17]结论的启发，我们设计了一种新颖的公式，能够增加他的准确性

\[c_{ui} = 1 + \alpha * g(R_{ui} - R^{max}/2) \tag{8}\]

这里g(*)可以是绝对值，平方差，甚至是对数函数。α（置信度）是一个控制相关量的超参数。这种机制可以控制极端的评分也能在一个合理的范围内，从而获得更高的信心。当然也可以用其他替代策略。

正则化

传统的矩阵分解通常使用l2范数正则化来计算潜在因素和偏差，以避免过于复杂的解。在这里，我们介绍另外两个正则化选项：Norm Chipping和Dropout。

Norm Clipping。对于pand Q，l2正则化是不可取的，因为它将使得用户和物品靠近原点。我们放松了对欧氏球的约束，并在每次更新后执行l2正则化裁剪，而不是最小化l2规则化。

\[\parallel P_u \parallel_2 \le l, \parallel Q_i \parallel_2 \le l \tag{9}\]

其中l控制欧几里得距离的大小。这两个约束作为正则化来限制$U_u$和$V_i$在l2正则化单位使得数据点不会过于分散[6,15]，从而避免维数灾难。这个操作通常在更新之后执行。每次迭代都有参数

Dropout。Dropout是解决神经网络中过拟合问题的一种简单有效的方法[34]。主要思想是在训练阶段丢掉一些神经元，以避免神经元过度适应。在这里，我们提出了一种新的欧几里得距离计算公式。欧氏距离是每个维度的距离的加法。为了防止尺寸之间的共同适应，我们建议随机丢弃一些尺寸并使用以下等式计算总距离

\[\parallel P_u + Q_i \parallel_2^2 = |p_{u1} - Q_{i1}|^2 + |p_{u2} - Q_{i2}|^2 + |P_{u3} - Q_{i3}|^2 + ... + |P_{uj} - Q{ij}|^2 + ... + |P_{uk} - Q_{ik}|^2\]

在上面的例子中，我们删除了第二个，第三个直到第二个，因此这些维度将不会对特定时期的距离预测产生影响。dropout维度在每个时代都会发生变化。请注意，dropout操作仅在训练期间执行。

在评分预估模型中，我们仍然利用具有正则率λ的l2正则来规范用户和物品偏差。

优化和推荐

我们使用Adagrad [4]优化算法训练评级预估和排名学习模型。Adagrad算法根据更新频率调整步长去调整参数。所以，它降低了调整学习速率。在推荐阶段，我们首先计算用户和物品之间的距离$\hat{Y}_{ui}$。对于预估阶段，我们使用以下规则定义评分：$\hat{R}_{ui} = R^{max} - \hat{Y}_{ui}$$。例如，假如$Y_ui = 4$，$R^{max} = 5$，预测评分为1。对于物品排序，我们直接按距离降序排列，从而把距离近的物品推荐给用户。

模型复杂性

FML对评分预估的复杂性与评分数成线性比例。它可以在$O（\mid\mathcal{K}\mid{k}）$中训练，其中k是潜在因子的维度和$\mid\mathcal{K}\mid$是观察到的数量。对于物品排序，由于涉及交互矩阵的所有物品，因此模型复杂度为$O（\mid{R}\mid k）$。具体而言，在Movielens 100K（NVIDIA TITAN XPascalGPU）上获得令人满意的推荐结果需要训练大约50分钟。对于FilmTrust上的物品排序，每一轮的计算时间约为15s，通常需要不到30个轮才能获得满意的结果。

实验

由于评分预测和物品排序通常使用不同的评估指标，因此我们单独评估这两个任务。我们实验评估所提出的方法主要是为了回答以下三个问题：

RQ1 是否FML在项目排名方面优于神经网络和度量学习方法吗？
RQ2 FML是否能够在基于MF和神经网络的模型中实现更准确的评分预估？
RQ3 超参数如何影响模型的性能？

评估物品排序

数据集说明。为了评估FML对隐式反馈的排序表现，我们对以下四个真实世界的数据集进行了实验。隐式反馈以与[13]相同的方式构建。

雅虎研究数据集。它由两个数据集组成：Ya-hoo电影和雅虎音乐。它们都是由雅虎研究联盟Webscope program4提供的。音乐偏好数据集是从Yahoo Music服务收集的。
FilmTrust。FilmTrust是由Guo等人从一个共享的网站上抓取来的。[9]。本文未使用信任信息。
EachMovie。EachMovie5是一个广泛用于推荐评估的基准电影数据集。

评估指标。为了评估排名的准确性和质量，我们采用了五个维度上的指标：Recall ，Precision，MeanAverage Precision（MAP），Mean Reciprocal Rank（MRR）和Normal malized Discounted Cumulative Gain（DNCG）。在实践中，在多个维度上获取较高评分的物品推荐给当前用户能获得更高的认可。MAP，MRR和NDCG是三个对排序性的度量，其中优先级较高的物品被优先考虑。因此，它们适用于评估列表质量[30]。MRR关注单一排名最高的相关物品。NDCG由折扣累积增益和理想折扣累积增益决定。所有评估指标都遵循着名的开源推荐项目6的实现，同样的实现也可以在LibRec7中找到。为了简明起见，省略了详细的定义，我们请读者[31]了解更多细节。

基线。我们将FML与以下经典和最近最先进的基线进行比较:

BPR [26]。这是一种通用的pairwise优化标准，可与MF一起使用。BPR优化标准旨在最大化负样本和正样本之间的差异
MRMF 它是隐式反馈的有效排名模型。它使用点积来建模用户物品交互模式。
NeuMF NeuMF将多层神经网络与广义矩阵分解相结合，并使用神经网络而不是点积来计算排名分数。它将排名问题视为一种分类任务，并通过最小化交叉熵损失来优化模型
CDAE CDAE从交互矩阵和自动编码器学习用户和物品分布的表示。去燥技术用于改进泛化和防止过度使用。在这里，我们使用逻辑损失来优化网络，因为据报道它可以在原始论文中获得最佳性能
CML CML是一个竞争基准。在这里，我们使用两种类型的损失：成对铰链损失和加权近似秩成对损失（WAPR）来训练该模型。请注意，由于负样本的预计算，WARP损失是计算密集的[41]。

总之，BPR和WRMF是基于矩阵分解的模型; NeuMF和CDAE是基于神经网络的模型;CML-PAIR和CML-WARP是基于度量学习的模型

实施细节。我们采用了My-medialite8 for BPR和WRMF的实现，以及作者发布的NeuMF 9的源代码。我们用Tensor-implemented实现了所有其他模型。我们使用80％的交互数据作为训练集，剩余的20％作为测试集，使用随机分组测试我们的模型，并报告平均结果。通过网格搜索确定超参数，以确保所有基线达到最佳性能。FML和CAL中的用户和项目向量的维度在{80,100,120,150,200}之间调整。学习率为FML设定为0.05。CML对和CML-WARP的边距最长为{0.5,1.0,1.5,2.0}。距离比例factora（公式3）设置为：2.25为FilmTrust，2.0为YahooMovie和EachMovie，在YahooMusic中$W_ui$,$R_ui$用于所有数据集。对于FilmTrust，置信度α设置为4，对于其他三个数据集，设置为1。Dropout 不会影响ranking表现，因此它不会用于项目ranking任务。

效果比较。根据多个标准排名指标对性能进行排名如表1所示。特别是，可以进行多次观察。首先，所提出的方法始终如一地在所有数据集上实现最佳性能，确定FML对项目排名的有效性。WRMF模型的整体性能提升高达20.8％。其次，虽然FML和CML都依赖于度量学习，但我们的模型仍然能够高达8.7％地完成CML，这表明FML可以更准确地反映用户和项目之间的距离关系。第三，基于欧几里德距离的模型（FML和CML）比基于点积的推荐器和神经网络模型表现更好，这与[15]中报道的结果一致。这也验证了使用欧氏距离捕获交互模式的优越性。第四，基于神经网络的模型CDAE是一个强大的基线。它通常优于BPR和WRMF，而NeuMF似乎比CDAE低。但是，仍然存在巨大的性能差距在这些模型和FML之间，这也表明添加非线性是不够的。

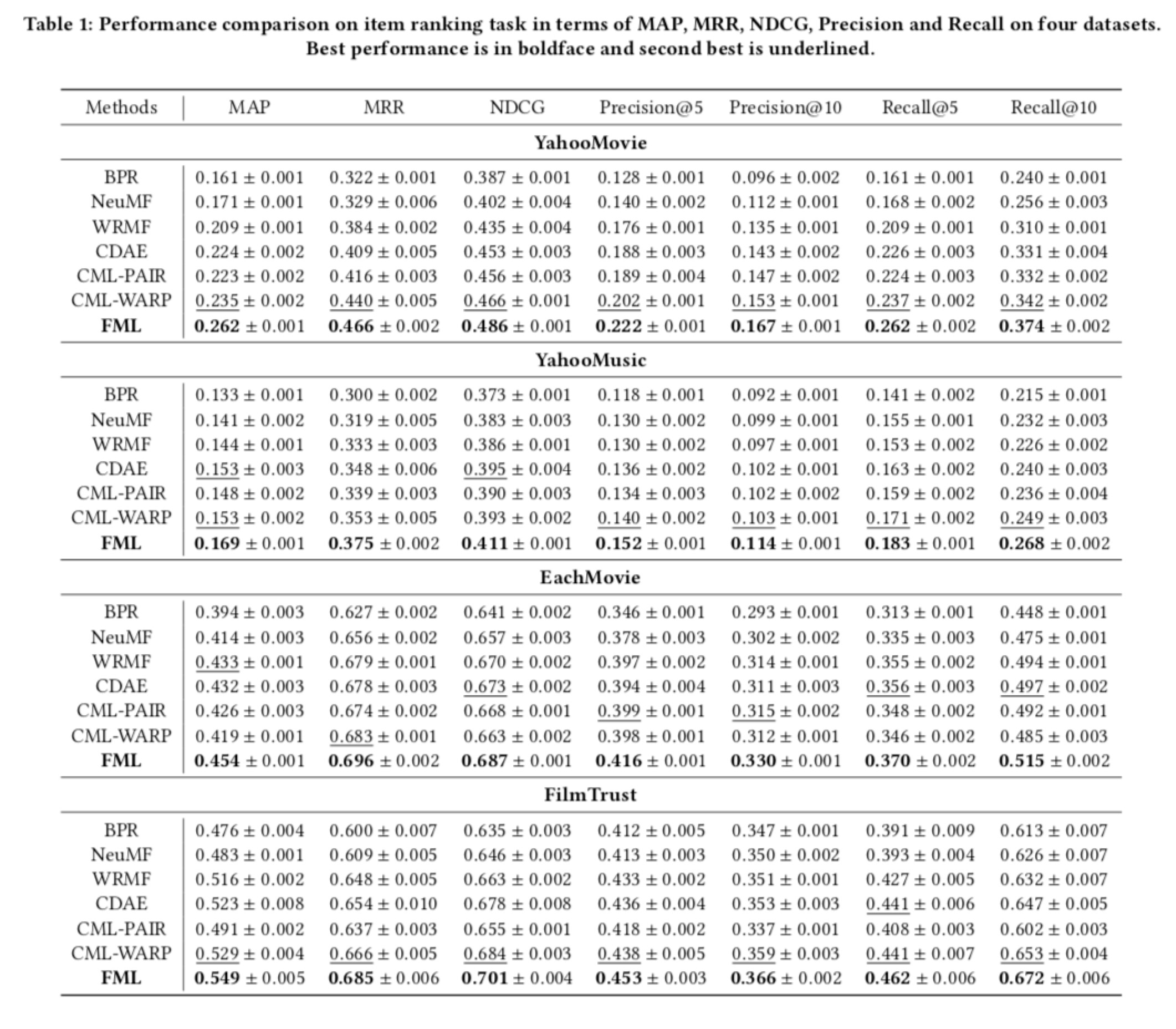
总的来说，这些观察结果证明了从度量向量空间因子化角度考虑推荐问题的优势。这也清楚地回答了RQ1。

第一次翻译论文，有点low大家将就着看，其实就前面算法原理部分有点意思，其他的可以直接看原论文，这里就不再啰嗦了。

矩阵分解的新思路

摘要

介绍

背景

推荐的矩阵分解

推荐中的深度模型

推荐中的度量学习