继续机器学习系列基础算法,逻辑回归
定义问题
首先我们依然是定义问题,逻辑回归是解决分类问题,而且是基本的二分类问题,比如经典的垃圾邮件判定,根据疾病的特征预测死亡率。比如现在我给出这样一个问题,基于邮件的两个特征值去判定邮件是不是为垃圾邮件,根据数据画出的分布图如下。蓝色表示不是垃圾邮件,红色表示是垃圾邮件,我们要做的是学习去拟合一个分类决策边界,然后就能根据这个模型预测。
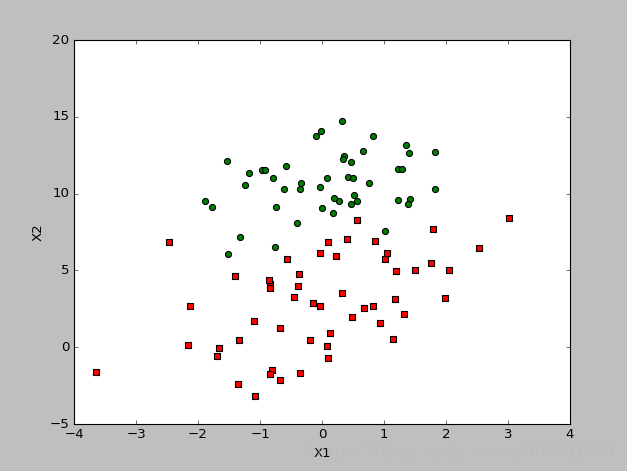
逻辑回归分布
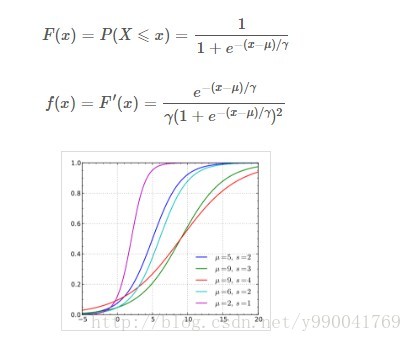
设X是连续的随机变量,X服从逻辑分布是指X具有下列分布函数和密度函数,在公式中,u为位置参数,r>0位形状参数,参考下面的图我们会发现,函数曲线是以(u, 0.5)中心对称,而r越小,中心附近增长越快。
就整个图形来说,曲线在中心附近增量最快,两端增长较慢,所以导函数图形是一个凹的钟形图。
逻辑回归模型
首先,定义几率(Odds),\(Odds=\frac{p}{1-p}\),既一件事发生的概率和不发生概率的比值,大于1则表示发生概率大,(0-1)表示不发生概率大,我们用一个性质很好的log函数就能够把线性回归到逻辑回归做了映射,可以看到log函数的值域是整个实数范围,对应于线性回归函数,而定义域\(x>0\),符合上面所有的定义。
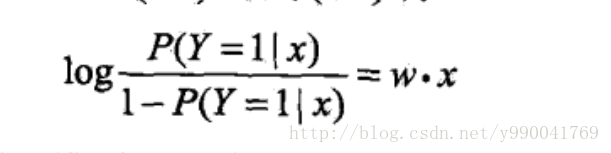
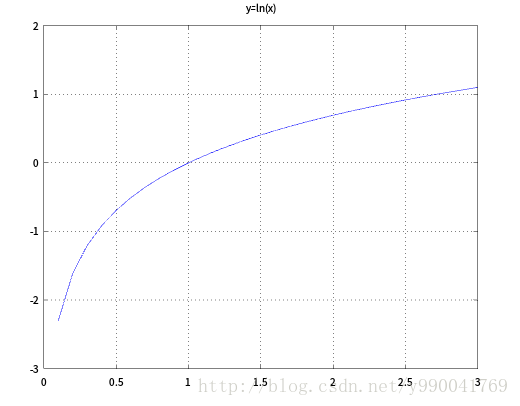
我们对上面公式进行变换,就是说y=1的对数几率是x的线性函数,就是我们所说的逻辑回归模型。换个角度来说,线性函数的值越接近正无穷,概率值越接近1,线性函数的值越接近负无穷,y越接近0,可以参照log函数图像。
对上面的公式进行变形,得到逻辑回归模型是一个如下的条件概率分布:
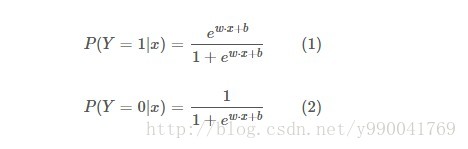
到这里我们就发现他其实就是给线性回归套上了一个log函数,然后让y的值分布在(0,1)之间
定义损失函数
我们现在要做的就是根据前面给出的观测样本去估计这些参数w,按照前面线性回归的思想我们定义均方误差损失函数,然后通过梯度下降法不断减小损失函数去迭代求解。
但是这里损失函数不能用均方误差,均方误差是最小二乘估计得到的,线性回归其误差属于正态分布,而逻辑回归是一个二项分布,这里要用一个最大似然估计定义损失函数,线性回归运用最大似然估计求解结果就是均方误差,有兴趣的可以推导一下。
最大似然估计在前面讲贝叶斯的时候写过,核心思想就是用现有的样本去找到一组参数使得现有样本的可能性最大,从统计学的角度讲就是使得所有观测样本的联合概率最大化,前提条件是所有样本之间必须相互独立,这也是逻辑回归的前提,就是问题必须是个二分类问题,两个只能选一个,在样本之间相互独立时,联合概率是各个样本出现概率的练乘积,既这个问题中的似然函数。
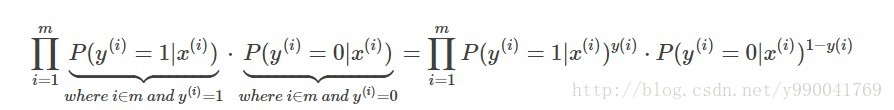
现在要做的就是求他的最大值,我们分析这个函数发现它是一个非凸函数,意思就是可能存在极小值,如果直接通过梯度下降法求解可能得到的不是最小值,之前线性回归中能直接求解因为它就是一个凸函数。因此我们对上面函数进行自然对数变换,将似然函数转换为对数似然函数,其中: \(g(x)=\frac{e^{θx}}{1+e^{θx}}\)
这里变换有两点要说明:
- 要做变换一方面是函数是非凸函数,另一方面是因为损失函数本身是一堆次方的乘积,这些乘积的结果会是一个很小的数,不好求直接最大值
- 函数变化是依赖对数函数的一些性质性质,一个是他是严格递增,另一个是乘积变加 \(ln(xy) = lnx + lny\),还有一个是指数变系数 \(lnx_{k} = {k}ln{x}\)
- 而且它的lnx导数正好是\(\frac{1}{2}\),正好能全部约掉,这个后面说
相对于求解似然函数的最大值,我们转化为目标转换的对偶问题,既代价函数\(J(θ)=−log(ℓ(θ))\)的最小值,因此我们就可以定义代价函数
\[cost=J(θ)=−log(ℓ(θ))=-\frac{1}{m}\sum_{i=1}^my(i)log(g(x))+(1−y(i))log(1−g(x))⟯\]有了代价函数,就可以迭代梯度下降了,梯度值推导一下
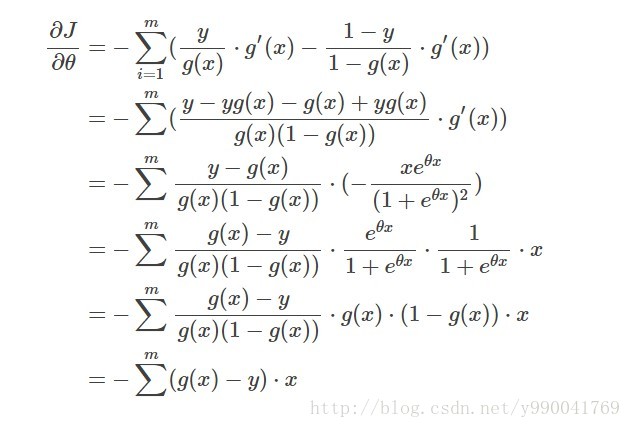
那么接下来就简单了,我们依然使用前面用过的类似梯度下降法去解决。这里因为我们要求解的是一个函数的最小值,梯度下降法可以参考之前线性回归 这里θ的更新函数是:
\[θ:=θ - α\sum_{i=1}^m(g(x)−y)⋅x\]总结
逻辑回归是一个判别模型,已知输入变量 \(x\) ,判别模型通过构建条件概率分布 \({\displaystyle P(y|x)}\) 预测 \(y\),它不关心\(x\)和\(y\) 之间的联合分布,与之对应的是生成模型,比如贝叶斯,它先对数据的联合分布建模,然后通过先验概率计算后验概率
逻辑回归的另一个变形就是多分类问题,通过softmax函数,使其能够处理多分类,这个后面研究研究在写
关于逻辑回归的优缺点:
优点: 实现简单,广泛的应用于工业问题上; 分类时计算量非常小,速度很快,存储资源低; 便利的观测样本概率分数; 对逻辑回归而言,多重共线性并不是问题,它可以结合L2正则化来解决该问题;
缺点: 当特征空间很大时,逻辑回归的性能不是很好; 容易欠拟合,一般准确度不太高 不能很好地处理大量多类特征或变量; 只能处理两分类问题(在此基础上衍生出来的softmax可以用于多分类),且必须线性可分; 对于非线性特征,需要进行转换;
线性回归的时候我们遗留了一个问题,即随机梯度下降的时候由于结果分布太离散而导致无法计算出一个最优解,这里对这个问题进行了优化,方法依然是前面说的从数据下手,我们每次取值取一个随机值,还有学习速率我们随着学习次数而减小,这样的好处是后面即使出现一些结果很离散或这噪声很大,对结果的影响很小,具体看代码。 首先我们先给出我们对于前面数据的学习结果,总体来看还是比较理想的:
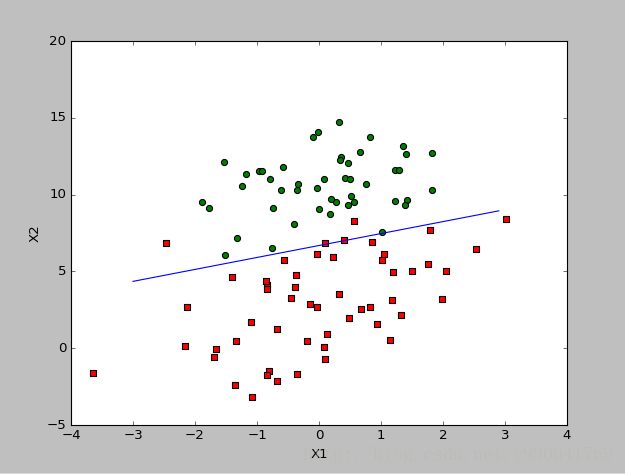
代码包括随机梯度下降,来自机器学习实战中:
#coding:utf-8
from numpy import *
def loadDataSet():
dataMat = []; labelMat = []
fr = open('testSet.txt')
for line in fr.readlines():
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
labelMat.append(int(lineArr[2]))
return dataMat,labelMat
def sigmoid(inX):
return 1.0/(1+exp(-inX))
def gradAscent(dataMatIn, classLabels):
dataMatrix = mat(dataMatIn) #convert to NumPy matrix
labelMat = mat(classLabels).transpose() #convert to NumPy matrix
m,n = shape(dataMatrix)
alpha = 0.001
maxCycles = 500
weights = ones((n,1))
print weights
for k in range(maxCycles): #heavy on matrix operations
h = sigmoid(dataMatrix*weights) #matrix mult
error = (labelMat - h) #vector subtraction
weights = weights + alpha * dataMatrix.transpose()* error #matrix mult
print "error: ",error
return weights
def plotBestFit(weights):
import matplotlib.pyplot as plt
dataMat,labelMat=loadDataSet()
dataArr = array(dataMat)
n = shape(dataArr)[0]
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
for i in range(n):
if int(labelMat[i])== 1:
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='green')
x = arange(-3.0, 3.0, 0.1)
y = (-weights[0]-weights[1]*x)/weights[2]
ax.plot(x, y)
plt.xlabel('X1'); plt.ylabel('X2');
plt.show()
def stocGradAscent0(dataMatrix, classLabels):
m,n = shape(dataMatrix)
alpha = 0.01
weights = ones(n) #initialize to all ones
for i in range(m):
h = sigmoid(sum(dataMatrix[i]*weights))
error = classLabels[i] - h
weights = weights + alpha * error * dataMatrix[i]
return weights
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
m,n = shape(dataMatrix)
weights = ones(n) #initialize to all ones
for j in range(numIter):
dataIndex = range(m)
for i in range(m):
alpha = 4/(1.0+j+i)+0.0001 #apha decreases with iteration, does not
randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant
h = sigmoid(sum(dataMatrix[randIndex]*weights))
error = classLabels[randIndex] - h
weights = weights + alpha * error * dataMatrix[randIndex]
del(dataIndex[randIndex])
return weights
def classifyVector(inX, weights):
prob = sigmoid(sum(inX*weights))
if prob > 0.5: return 1.0
else: return 0.0
def colicTest():
frTrain = open('horseColicTraining.txt'); frTest = open('horseColicTest.txt')
trainingSet = []; trainingLabels = []
for line in frTrain.readlines():
currLine = line.strip().split('\t')
lineArr =[]
for i in range(21):
lineArr.append(float(currLine[i]))
trainingSet.append(lineArr)
trainingLabels.append(float(currLine[21]))
trainWeights = stocGradAscent1(array(trainingSet), trainingLabels, 1000)
errorCount = 0; numTestVec = 0.0
for line in frTest.readlines():
numTestVec += 1.0
currLine = line.strip().split('\t')
lineArr =[]
for i in range(21):
lineArr.append(float(currLine[i]))
if int(classifyVector(array(lineArr), trainWeights))!= int(currLine[21]):
errorCount += 1
errorRate = (float(errorCount)/numTestVec)
print "the error rate of this test is: %f" % errorRate
return errorRate
def multiTest():
numTests = 10; errorSum=0.0
for k in range(numTests):
errorSum += colicTest()
print "after %d iterations the average error rate is: %f" % (numTests, errorSum/float(numTests))
if __name__ == '__main__':
dataArr, labelMat = loadDataSet()
weight = gradAscent(dataArr, labelMat)
#weight = stocGradAscent1(array(dataArr), labelMat)
print weight
plotBestFit(weight.getA()) #getA mat to arr
#plotBestFit(weight) #getA mat to arr
#multiTest()